题目内容
16.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左右焦点分别为F1,F2,点P在双曲线的右支上,且|PF1|=5|PF2|,则此双曲线的离心率的取值范围是( )| A. | (1,$\sqrt{3}$] | B. | (1,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (3,+∞) |
分析 由双曲线的定义可得|PF1|-|PF2|=4|PF2|=2a,再根据点P在双曲线的右支上,可得|PF2|≥c-a,从而求得此双曲线的离心率e的取值范围.
解答 解:∵|PF1|=5|PF2|,
∴由双曲线的定义可得|PF1|-|PF2|=4|PF2|=2a,
∴|PF2|=$\frac{1}{2}$a,
∵点P在双曲线的右支上,
∴|PF2|≥c-a,即$\frac{1}{2}$a≥c-a,即$\frac{3}{2}$a≥c,
∴e=$\frac{c}{a}$≤$\frac{3}{2}$,
∵e>1,
∴1<e≤$\frac{3}{2}$,
∴双曲线的离心率e的取值范围为(1,$\frac{3}{2}$].
故选B.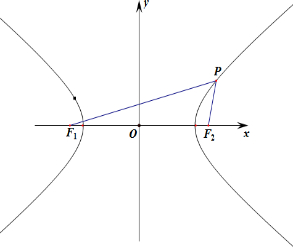
点评 本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,考查学生的计算能力,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
7.已知实数a,b满足2<a<b<3,下列不等关系中一定成立的是( )
| A. | a3+15b>b3+15a | B. | a3+15b<b3+15a | C. | b•2a>a•2b | D. | b•2a<a•2b |
11.设集合M={x|(x-1)(x+2)<0},N={x∈Z||x|≤2},则M∩N=( )
| A. | {-1,0} | B. | {0,1} | C. | {-1,0,1} | D. | {0,1,2} |
1.由于空气污染严重,某工厂生产了两种供人们外出时便于携带的呼吸装置,其质量按测试指标划分:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种装置各100件进行检测,检测结果统计如下:
(Ⅰ)试分别估计装置甲、装置乙为合格品的概率;
(Ⅱ)生产一件装置甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件装置乙,若是合格品可盈利50元,若是次品则亏损10元.在(Ⅰ)的条件下,
(1)记X为生产一件装置甲和生产一件装置乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件装置乙所获得的利润不少于140元的概率.
| 测试指标 | [70,76] | [76,82] | [82,88] | [88,94] | [94,100] |
| 装置甲 | 8 | 12 | 40 | 32 | 8 |
| 装置乙 | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件装置甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件装置乙,若是合格品可盈利50元,若是次品则亏损10元.在(Ⅰ)的条件下,
(1)记X为生产一件装置甲和生产一件装置乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件装置乙所获得的利润不少于140元的概率.
6.已知集合A={x|x2-2x-3≥0},B={x|-2≤x≤2},则A∩B=( )
| A. | {x|1≤x≤2} | B. | {x|-1≤x≤2} | C. | {x|-1≤x≤1} | D. | {x|-2≤x≤-1} |