题目内容
6．给出下列几种说法：①经过圆柱任意两条母线的截面是一个矩形；②连接圆柱上、下底面圆周上两点的线段是圆柱的母线；③圆柱的任意两条母线互相平行，其中正确的个数为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 矩形绕着它的一条边AG所在的直线旋转一周，得到的几何体，叫做圆柱，DD'不管转到任何位置，都叫母线．由定义及概念，可判断②；再由性质，截面的形状，侧面展开图，即可判断①③．
解答 
解：如图矩形绕着它的一条边AG所在的直线旋转一周，得到的几何体，叫做圆柱，DD'不管转到任何位置，都叫母线．
故①经过圆柱任意两条母线的截面是一个矩形，则①对；
由母线定义可知②错；
由圆柱的性质可知③对；
故正确的命题的个数为2，
故选：C．
点评 本题考查圆柱的定义，性质和侧面展开图，以及截面等概念，属于基础题．
练习册系列答案
相关题目
16．在正三棱柱ABC-A1B1C1中，已知AB=2，CC1=$\sqrt{2}$，则异面直线AB1和BC1所成角的余弦值为（ ）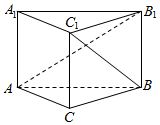
| A． | 0 | B． | $\frac{\sqrt{42}}{7}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{1}{2}$ |
如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，则直线EF与正方体的六个面所在的平面相交的平面个数为（ ）
14．F为双曲线Г：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，若Г上存在一点P使得△OPF为等边三角形（O为坐标原点），则Г的离心率e为（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}+1}{2}$ | C． | $\sqrt{3}+1$ | D． | 2 |