题目内容
对于数列{cn},如果存在各项均为正整数的等差数列{an}和各项均为正整数的等比数列{bn},使得cn=an+bn,则称数列{cn}为“DQ数列”.已知数列{en}是“DQ数列”,其前5项分别是:3,6,11,20,37,则en= .
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:设公差和公比分别为d、q,由题意可得a1,b1,d,q的方程组,解方程组由等差数列和等比数列的通项公式可得.
解答:
解:由题意设等差数列{an}和等比数列{bn}的公差和公比分别为d、q,
由题意可得a1+b1=3,a1+d+b1q=6,a1+2d+b1q2=11,a1+3d+b1q3=20,
结合数列的各项均为正整数可解得a1=1,b1=2,d=1,q=2,
∴en=an+bn=1+(n-1)×1+2×2n-1=n+2n,
故答案为:n+2n
由题意可得a1+b1=3,a1+d+b1q=6,a1+2d+b1q2=11,a1+3d+b1q3=20,
结合数列的各项均为正整数可解得a1=1,b1=2,d=1,q=2,
∴en=an+bn=1+(n-1)×1+2×2n-1=n+2n,
故答案为:n+2n
点评:本题考查数列的基本概念,涉及等差数列和等比数列的通项公式,属基础题.

练习册系列答案
相关题目
函数y=sin(2x+
)的图象经过下列平移,可以得到偶函数图象的是( )
| π |
| 3 |
A、向右平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向左平移
|
已知an=3n+1,n∈N*,如果执行如图的程序框图,那么输出的S等于( )


| A、17.5 | B、35 |
| C、175 | D、350 |
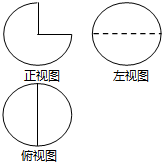 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是