题目内容
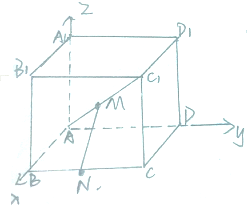 在棱长为1的正方体ABCD-A1B1C1D1中,动点M在线段AC1上,动点N在线段BC上,建立空间直角坐标系(如图所示),求线段MN长度最小值,以及此时点M,N的坐标.
在棱长为1的正方体ABCD-A1B1C1D1中,动点M在线段AC1上,动点N在线段BC上,建立空间直角坐标系(如图所示),求线段MN长度最小值,以及此时点M,N的坐标.考点:点、线、面间的距离计算,空间中的点的坐标
专题:空间位置关系与距离
分析:线段MN长度最小时,MN是BC和AC1的公垂直线段,由此利用向量法能求出线段MN长度最小值,以及此时点M,N的坐标.
解答:
解:由已知得B(1,0,0),C(1,1,0),
A(0,0,0),C1(1,1,1),
=(0,1,0),
=(1,1,1),
设
=m
,
=n
,
则
=(0,m,0),N(1,m,0),
=(n,n,n),M(n,n,n),
∴
=(n-1,n-m,n),
∵线段MN长度最小,∴MN⊥BC,且MN⊥AC1,
∴
,
∴m=n=
,
∴线段MN长度最小值为|
|min=
=
,
此时M(
,
,
),N(1,
,0).

A(0,0,0),C1(1,1,1),
| BC |
| AC1 |
设
| BN |
| BC |
| AM |
| AC1 |
则
| BN |
| AM |
∴
| NM |
∵线段MN长度最小,∴MN⊥BC,且MN⊥AC1,
∴
|
∴m=n=
| 1 |
| 2 |
∴线段MN长度最小值为|
| NM |
(-
|
| ||
| 2 |
此时M(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查线段MN长度最小值以及此时点M,N的坐标的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
不等式组
的解集记为D,若?(x,y)∈D,则( )
|
| A、x+2y≥-2 |
| B、x+2y≥2 |
| C、x-2y≥-2 |
| D、x-2y≥2 |
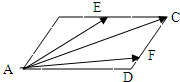 如图所示,在平行四边形ABCD中,E为BC的中点,F为CD的四分之一点,设
如图所示,在平行四边形ABCD中,E为BC的中点,F为CD的四分之一点,设