题目内容
数列{an}中,a1=2,an+1=an+cn(c是常数,n=1,2,3,…)),且a1,a2,a3成公比不为1的等比数列,则{an}的通项公式是 .
考点:数列递推式
专题:等差数列与等比数列
分析:根据等比数列的通项公式求出c,然后利用累加法即可得到结论.
解答:
解:∵a1=2,an+1=an+cn,
∴a2=a1+c=2+c,a3=a2+2c=2+3c,
∵a1,a2,a3成公比不为1的等比数列,
∴a22=a1a3,即(2+c)2=2(2+3c),
即c2=2c,解得c=2或c=0舍去,
则an+1=an+2n,即an+1-an=2n,
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+2+4+…+2(n-1)=2+
×(n-1)=n2-n+2,
故答案为:n2-n+2
∴a2=a1+c=2+c,a3=a2+2c=2+3c,
∵a1,a2,a3成公比不为1的等比数列,
∴a22=a1a3,即(2+c)2=2(2+3c),
即c2=2c,解得c=2或c=0舍去,
则an+1=an+2n,即an+1-an=2n,
则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+2+4+…+2(n-1)=2+
| 2+2(n-1) |
| 2 |
故答案为:n2-n+2
点评:本题主要考查等比数列的通项公式,以及利用累加法求通项公式.

练习册系列答案
相关题目
设双曲线
-
=1(a>0)的渐近线方程为3x±2y=0,则a的值为( )
| x2 |
| a2 |
| y2 |
| 9 |
| A、4 | B、3 | C、2 | D、1 |
由直线x=-
,x=-2,曲线y=
及x轴所围图形的面积是( )
| 1 |
| 2 |
| 1 |
| x |
A、
| ||
B、
| ||
C、
| ||
| D、2ln2 |
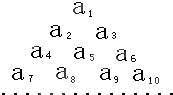 已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,4)=
已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,4)=