题目内容
已知变量x,y满足约束条件
,则目标函数z=3x-y+3的取值范围为( )
|
A、[-
| ||
B、[
| ||
| C、[-2,3] | ||
| D、[1,6] |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组表示的平面区域;作出目标函数对应的直线;结合图象根据截距的大小进行判断,从而得出目标函数z=3x-y+3的取值范围.
解答:
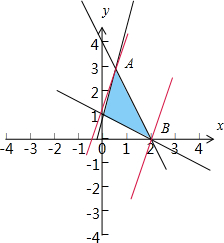 解:∵变量x,y满足约束条件
解:∵变量x,y满足约束条件
,
可行域如图:
目标函数为:z=3x-y+3,
直线4x-y+1=0与2x+y-4=0交于点A(
,3),
直线2x+y-4=0与x+2y-2=0交于点B(2,0),
分析可知z在点A处取得最小值,zmin=3×
-3+3=
,
z在点B处取得最大值,zmax=3×2-0+3=9,
∴
≤z≤9,
故选:B.
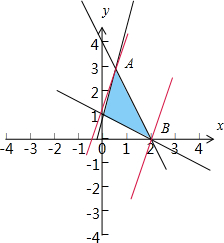 解:∵变量x,y满足约束条件
解:∵变量x,y满足约束条件
|
可行域如图:
目标函数为:z=3x-y+3,
直线4x-y+1=0与2x+y-4=0交于点A(
| 1 |
| 2 |
直线2x+y-4=0与x+2y-2=0交于点B(2,0),
分析可知z在点A处取得最小值,zmin=3×
| 1 |
| 2 |
| 3 |
| 2 |
z在点B处取得最大值,zmax=3×2-0+3=9,
∴
| 3 |
| 2 |
故选:B.
点评:本题考查画不等式组表示的平面区域、考查数形结合求函数的最值,此题是一道中档题,有一定的难度,画图是关键;

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
函数f(x)=x3-6x2+9x-10=0的零点个数是( )
| A、3 个 |
| B、2 个 |
| C、1 个 |
| D、0 个 |
已知抛物线y=ax2+bx+c(a≠0)的对称轴在y轴的左侧,其中a,b,c∈{-3,-2,-1,0,1,2,3},在这些抛物线中,若随机变量ξ=|a-b|的取值,则ξ的数学期望E(ξ)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
双曲线5x2+ky2=5的一个焦点是(
,0),那么实数k的值为( )
| 6 |
| A、-25 | B、25 | C、-1 | D、1 |
已知椭圆
+
=1,则以点P(4,2)为中点的弦所在的直线方程为( )
| x2 |
| 36 |
| y2 |
| 9 |
| A、2x+y-8=0 |
| B、2x-y-8=0 |
| C、x+2y-8=0 |
| D、2y+x+8=0 |
若实数m满足0<m<4,则曲线
-
=1与曲线
-
=1的( )
| x2 |
| 12 |
| y2 |
| 4-m |
| x2 |
| 12-m |
| y2 |
| 4 |
| A、实半轴长相等 |
| B、虚半轴长相等 |
| C、离心率相等 |
| D、焦距相等 |




