题目内容
10.已知sinx=$\frac{3}{5}$,$x∈(\frac{π}{2},π)$,求cos2x和$tan(x+\frac{π}{4})$值.分析 由二倍角的余弦函数公式化简cos2x,得到关于sinx的关系式,把sinx的值代入即可求出值,由sinx的值及x的范围,利用同角三角函数间的基本关系求出cosx的值,进而求出tanx的值,然后把所求的式子利用两角和的正切函数公式及特殊角的三角函数值化简后,将tanx的值代入即可求出值.
解答 解:由sinx=$\frac{3}{5}$,
得cos2x=1-2sin2x=$1-2×\frac{9}{25}=\frac{7}{25}$.
又sinx=$\frac{3}{5}$,$x∈(\frac{π}{2},π)$,
∴cosx=-$\frac{4}{5}$,
∴$tanx=\frac{sinx}{cosx}=-\frac{3}{4}$.
∴$tan(x+\frac{π}{4})$=$\frac{tanx+1}{1-tanx}=\frac{-\frac{3}{4}+1}{1+\frac{3}{4}}=\frac{1}{7}$.
点评 本题考查运用二倍角的余弦函数公式及同角三角函数间的基本关系化简求值,灵活运用两角和的正切函数公式及特殊角的三角函数值化简求值,是基础题.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
5.设函数y=f(x)的定义域为D,若对于任意x1,x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x+sinπx-3的某一个对称中心,并利用对称中心的上述定义,可得到$f(\frac{1}{2017})+f(\frac{2}{2017})+f(\frac{3}{2017})+…+f(\frac{4032}{2017})+f(\frac{4033}{2017})$的值为( )
| A. | -4033 | B. | 4033 | C. | 8066 | D. | -8066 |
19.函数f(x)=|ln x|-x2的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
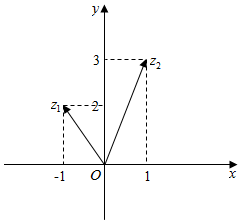 如图,已知向量$\overrightarrow{O{Z}_{1}}$与$\overrightarrow{O{Z}_{2}}$对应的复数是z1与z2
如图,已知向量$\overrightarrow{O{Z}_{1}}$与$\overrightarrow{O{Z}_{2}}$对应的复数是z1与z2