题目内容
20.圆${C_1}:{(x+1)^2}+{(y+2)^2}=4$与圆${C_2}:{(x-1)^2}+{(y+1)^2}=9$的位置关系是( )| A. | 内切 | B. | 相交 | C. | 外切 | D. | 相离 |
分析 求出两圆的圆心,半径,计算圆心距,比较圆心距与两半径的关系得出结论.
解答 解:圆C1的圆心为(-1,-2),半径为r1=2,
圆C2的圆心为(1,-1),半径为r2=3,
两圆的圆心距d=$\sqrt{(-1-1)^{2}+(-2+1)^{2}}$=$\sqrt{5}$,
∴r2-r1<d<r1+r2,
∴两圆相交.
故选B.
点评 本题考查了圆的标准方程,圆与圆的位置关系,属于基础题.

练习册系列答案
相关题目
8.数列{an}的通项公式an=ncos$\frac{nπ}{2}$,其前n项和为Sn,则S2013等于( )
| A. | 1006 | B. | 2012 | C. | 503 | D. | 0 |
12.已知等比数列{an}各项均为正数,公比为q,满足an+1<an,a2a8=6,a4+a6=5,则q2=( )
| A. | $\frac{5}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
10.复数(i-$\frac{1}{i}$)3的虚部是( )
| A. | -8 | B. | -8i | C. | 8 | D. | 8i |
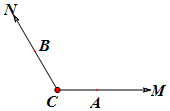 已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.
已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.