题目内容
2.正△ABC的三个顶点都在球O的球面上,AB=AC=2,若三棱锥O-ABC的体积为2,则该球的表面积为$\frac{160π}{3}$.分析 根据题意求出正△ABC的面积以及点O到底面的距离,再求出球的半径,即可求出球的表面积.
解答 解:正△ABC的三个顶点都在以O为球心的球面上,
且AB=AC=BC=2,
取BC中点D,连结AD,OD,
过O作OE⊥平面ABC,则OE∩AD=E,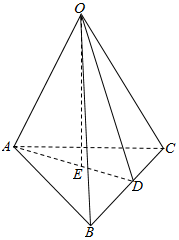 如图所示;
如图所示;
∴AD=$\sqrt{{2}^{2}{-1}^{2}}$=$\sqrt{3}$,
AE=$\frac{2}{3}$AD=$\frac{2\sqrt{3}}{3}$,
S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
∵三棱锥O-ABC的体积为2,
∴$\frac{1}{3}$×$\sqrt{3}$×OE=2,
解得OE=2$\sqrt{3}$,
∴球的半径为OA=$\sqrt{{OE}^{2}{+AE}^{2}}$=$\sqrt{{(2\sqrt{3})}^{2}{+(\frac{2\sqrt{3}}{3})}^{2}}$=$\sqrt{\frac{40}{3}}$,
∴球的表面积为S=4π×OA2=$\frac{160π}{3}$.
故答案为:$\frac{160π}{3}$.
点评 本题考查了球的表面积求法问题,也考查了空间想象能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.2017年实验中学要给三个班级补发8套教具,先将其分成3堆,其中一堆4个,另两堆每堆2个,一共有多少种不同分堆方法( )
| A. | C${\;}_{8}^{4}$C${\;}_{4}^{2}$C${\;}_{2}^{2}$ | B. | C${\;}_{3}^{1}$C${\;}_{8}^{2}$ | ||
| C. | $\frac{{C}_{8}^{4}{C}_{4}^{2}}{{A}_{2}^{2}}$ | D. | $\frac{{C}_{8}^{4}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{3}^{3}}$ |
14.平行于直线x+2y+1=0,且与圆x2+y2=5相切的直线的方程是( )
| A. | $x+2y+\sqrt{5}=0$或$x+2y-\sqrt{5}=0$ | B. | $x-2y+\sqrt{5}=0$或$x-2y-\sqrt{5}=0$ | ||
| C. | x+2y+5=0或x+2y-5=0 | D. | x-2y+5=0或x-2y-5=0 |
12.已知等比数列{an}各项均为正数,公比为q,满足an+1<an,a2a8=6,a4+a6=5,则q2=( )
| A. | $\frac{5}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
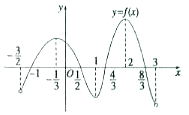 函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).
函数y=f(x)在其定义域$[{-\frac{3}{2},3}]$内可导,其图象如图所示,记y=f(x)的导函数为y=f'(x),则不等式f′(x)≤0的解集是[-$\frac{1}{3}$,1]∪[2,3).