题目内容
已知函数f(x)=ex-2x(e为自然对数的底数)
(1)求函数f(x)的单调区间
(2)若存在x∈[
,2]使不等式f(x)<mx成立,求实数m的取值范围.
(1)求函数f(x)的单调区间
(2)若存在x∈[
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)先求出函数的导数,令f′(x)=0,解得x=ln2,从而求出函数的单调区间;
(Ⅱ)问题转化为求m>(
)的最小值.令g(x)=
-2,通过求导得到函数g(x)的最小值,从而求出m的范围.
(Ⅱ)问题转化为求m>(
| ex-2x |
| x |
| ex |
| x |
解答:
解:(Ⅰ)f′(x)=ex-2,
令f′(x)=0,即ex-2=0,解得x=ln2,
x∈(-∞,ln2)时,f′(x)<0,x∈(ln2,+∞)时,f′(x)>0,
∴f(x)的单调递减区间为(-∞,ln2),单调递增区间为(ln2,+∞).
(Ⅱ)由题意知?x∈[
, 2]使f(x)<mx成立,
即?x∈[
, 2]使m>
成立;
所以m>(
)的最小值.
令g(x)=
-2,g′(x)=
,
所以g(x)在[
, 1]上单调递减,在[1,2]上单调递增,
则g(x)min=g(1)=e-2,所以m∈(e-2,+∞).
令f′(x)=0,即ex-2=0,解得x=ln2,
x∈(-∞,ln2)时,f′(x)<0,x∈(ln2,+∞)时,f′(x)>0,
∴f(x)的单调递减区间为(-∞,ln2),单调递增区间为(ln2,+∞).
(Ⅱ)由题意知?x∈[
| 1 |
| 2 |
即?x∈[
| 1 |
| 2 |
| ex-2x |
| x |
所以m>(
| ex-2x |
| x |
令g(x)=
| ex |
| x |
| (x-1)ex |
| x2 |
所以g(x)在[
| 1 |
| 2 |
则g(x)min=g(1)=e-2,所以m∈(e-2,+∞).
点评:本题考查了函数的单调性,函数的最值问题,考查了导数的应用,考查转化思想,是一道中档题.

练习册系列答案
相关题目
已知抛物线y2=2px(p>0)的准线与圆x2+y2-4x-5=0相切,则p的值为( )
| A、10 | B、6 | C、4 | D、2 |
已知某一随机变量X的分布列如下,则m的值为( )
| X | 4 | 7 | 9 |
| P | 0.5 | m | 0.4 |
| A、0.4 | B、0.3 |
| C、0.2 | D、0.1 |
已知函数f(x)=2lnx+1的图象与直线y=2x-a恰好有一个交点,设g(x)=ex-x2+a,当x∈[1,2]时,不等式-m≤g(x)≤m2-4恒成立,则实数m的取值范围是( )
A、(-∞,
| ||
B、[
| ||
C、[-e,
| ||
D、[
|
有3位同学参加测试,假设每位同学能通过测试的概率都是
,且各人能否通过测试是相互独立的,则至少有一位同学能通过测试的概率为( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
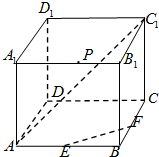 在长方体ABCD-A1B1C1D1中,AB=AA1=4,BC=3,E、F分别是所在棱AB、BC的中点,点P是棱A1B1上的动点,联结EF,AC1.如图所示.
在长方体ABCD-A1B1C1D1中,AB=AA1=4,BC=3,E、F分别是所在棱AB、BC的中点,点P是棱A1B1上的动点,联结EF,AC1.如图所示.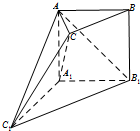 如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.
如图,在多面体ABC-A1B1C1中,侧面AA1B1B⊥底面A1B1C1,四边形AA1B1B是矩形,A1C1=A1B1,BC∥B1C1,B1C1=2BC.