Question

过双曲线

x2

a2

-

y2

b2

=1（a＞0，b）的右焦点F（c，0）的直线交双曲线于A、B两点，交y轴于点P，则有

|PA|

|AF|

-

|PB|

|BF|

为定值

2ac

b2

，类比双曲线的这一结论，在椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）中，

|PA|

|AF|

+

|PB|

|BF|

也为定值，则这个定值为（　　）

• A、

  2a2

  b2

• B、

  2ac

  b2

• C、

  2b2

  a2

• D、

  2bc

  a2

Answer 1

考点：双曲线的简单性质

专题：计算题,圆锥曲线的定义、性质与方程

分析：双曲线的这一结论，在椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）中，|

|PA|

|AF|

-

|PB|

|BF|

|也为定值，且为

2a2

b2

．设出直线方程，联立椭圆方程，消去y，得到x的方程，运用韦达定理，以及共线向量的坐标表示，化简整理，即可得到定值．

解答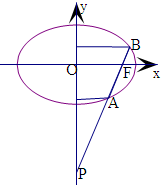： 解：双曲线的这一结论，在椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）中，
|

|PA|

|AF|

-

|PB|

|BF|

|也为定值，且为

2a2

b2

．
理由如下：设椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的焦点F（c，0），
过F的直线为y=k（x-c），代入椭圆方程，可得
（b²+a²k²）x²-2a²k²cx+a²k²c²-a²b²=0，
设A（x₁，y₁），B（x₂，y₂），
则x₁+x₂=

2a2k2c

b2+a2k2

，x₁x₂=

a2k2c2-a2b2

b2+a2k2

，
则|

|PA|

|AF|

-

|PB|

|BF|

|=|

x1

c-x1

-

x2

x2-c

|=|

c(x1+x2)-2x1x2

c2-c(x1+x2)+x1x2

|
=|

2a2k2c2 b2+a2k2 - 2(a2k2c2-a2b2) b2a2k2

c2- 2a2k2c2 b2+a2k2 + a2k2c2-a2b2 b2+a2k2

|=|

2a2b2

(c2-a2)b2

|=

2a2

b2

，
故选A．

点评：本题考查椭圆方程的运用，考查直线方程和椭圆方程联立，运用韦达定理，考查化简整理的能力，具有一定的运算量，属于中档题和易错题．