题目内容
10.经过函数$y=\frac{1}{x}$上一点M引切线l与x轴、y轴分别交于点A和点B,O为坐标原点,记△OAB的面积为S,则S=2.分析 设P(x0,y0)为$y=\frac{1}{x}$上任一点,过点P作曲线C的切线l,利用导数可求得切线l的斜率及方程,从而可求得l与两坐标轴交于A,B两点的坐标,继而可求△OAB的面积.
解答 解:设P(x0,y0)为$y=\frac{1}{x}$上任一点,则y0=$\frac{1}{{x}_{0}}$.
∵y′=-$\frac{1}{{x}^{2}}$,设过$y=\frac{1}{x}$上一点P的切线l的斜率为k,
则k=-$\frac{1}{{x}_{{0}^{2}}}$,
∴切线l的方程为:y-y0=-$\frac{1}{{x}_{{0}^{2}}}$(x-x0),
∴当x=0时,y=$\frac{1}{{x}_{0}}$+y0=$\frac{2}{{x}_{0}}$,即B(0,$\frac{2}{{x}_{0}}$);
当y=0时,x=y0•x02+x0=$\frac{1}{{x}_{0}}$•x02+x0=2x0,即A(2x0,0);
∴S△OAB=$\frac{1}{2}$|OA|•|OB|=$\frac{1}{2}$×|2x0|•|$\frac{2}{{x}_{0}}$|=2.
故答案为:2
点评 本题考查利用导数求过$y=\frac{1}{x}$上一点P的切线l的斜率,考查直线的方程及截距,考查三角形的面积公式,属于中档题.

练习册系列答案
相关题目
20.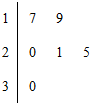 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
( )
 某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为
某车间共有6名工人,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.从该车间6名工人中,任取2人,则至少有1名优秀工人的概率为 ( )
| A. | $\frac{8}{15}$ | B. | $\frac{4}{9}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{9}$ |
1.把-1485°转化为α+k•360°(0°≤α<360°,k∈Z)的形式是( )
| A. | 45°-4×360° | B. | -45°-4×360° | C. | -45°-5×360° | D. | 315°-5×360° |
15.函数f(x)=x3-15x的某个零点所在的一个区间是( )
| A. | (-2,0) | B. | (-1,1) | C. | (0,2) | D. | (1,3) |
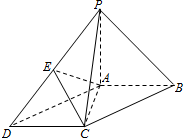 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且AB=AC=$\frac{1}{2}$PA=1,点E是PD的中点.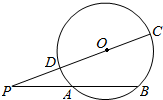 自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,
自圆O外一点P引圆O的两条割线PAB和PDC,如图所示,其中割线PDC过圆心O.AB=$\sqrt{2}$OA,PD=$\sqrt{3}$,∠P=15°,