题目内容
不等式-2x2+x+3＜0的解集是（ ）
| A、{x|x＜-1} | ||
B、{x|x＞
| ||
C、{x|x-1＜x＜
| ||
D、{x|x＜-1或x＞
|
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：按照解一元二次不等式的基本步骤解答，即可得出正确的答案．
解答：
解：不等式-2x2+x+3＜0可化为
2x2-x-3＞0，
即（2x-3）（x+1）＞0；
解得x＜-1，或x＞
；
∴不等式的解集是{x|x＜-1，或x＞
}．
故选：D．
2x2-x-3＞0，
即（2x-3）（x+1）＞0；
解得x＜-1，或x＞
| 3 |
| 2 |
∴不等式的解集是{x|x＜-1，或x＞
| 3 |
| 2 |
故选：D．
点评：本题考查了一元二次不等式的求解问题，解题时应按照解一元二次不等式的基本步骤解答即可，基础题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
1001101（2）与下列哪个值相等（ ）
| A、125（7） |
| B、136（6） |
| C、177（5） |
| D、115（8） |
设n=
（4sinx+cosx）dx，则二项式（x-
）n的展开式中x的系数为（ ）
| ∫ |
0 |
| 1 |
| x |
| A、4 | B、10 | C、5 | D、6 |
设复数z=1-2i（i为虚数单位），则复数z的虚部为（ ）
| A、-2 | B、2 | C、-2i | D、2i |
设复数z=
（i为虚数单位），z的共轭复数为
，则在复平面内i
对应当点的坐标为（ ）
| 2 |
| -1-i |
. |
| z |
. |
| z |
| A、（1，1） |
| B、（-1，1） |
| C、（1，-1） |
| D、（-1，-1） |
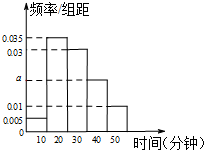某学校为调查高一新生上学路程所需要的时间（单位：分钟），从高一年级新生中随机抽取100名新生按上学所需时间分组：第1组（0，10]，第2组（10，20]，第3组（20，30]，第4组（30，40]，第5组（40，50]，得到的频率分布直方图如图所示．
已知函数f（x）=
如图在单位圆中，