题目内容
9.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且经过点(2,0)(Ⅰ)求椭圆C的方程
(Ⅱ)若与坐标轴不垂直的直线l经过椭圆C的左焦点F(-c,0),且与椭圆C交于不同两点A,B,问是否存在常数λ,(λ为实数),使|AB|=λ|AF||BF|恒成立,若存在,请求出λ的值,若不存在,请说明理由.
分析 (Ⅰ)由题意,a=2,c=$\sqrt{3}$,b=1,即可求椭圆C的方程;
(Ⅱ)直线l的方程为x=my-$\sqrt{3}$,与椭圆方程联立,消去x得:(m2+4)y2-2$\sqrt{3}$my-1=0,利用弦长公式、一元二次方程的根与系数的关系,即可得出结论.
解答 解:(Ⅰ)由题意,a=2,c=$\sqrt{3}$,b=1,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1;
(Ⅱ)F(-$\sqrt{3}$,0),设A(x1,y1),B(x2,y2),直线l的方程为x=my-$\sqrt{3}$,
与椭圆方程联立,消去x得:(m2+4)y2-2$\sqrt{3}$my-1=0,
y1+y2=$\frac{2\sqrt{3}m}{{m}^{2}+4}$,y1y2=-$\frac{1}{{m}^{2}+4}$,
∴|AB|=$\sqrt{1+{m}^{2}}$|y1-y2|=$\frac{4({m}^{2}+1)}{{m}^{2}+4}$,
∵|AF||BF|=|y1y2|(1+m2)=$\frac{1+{m}^{2}}{{m}^{2}+4}$,
∴|AB|=4|AF||BF|,
∴存在常数λ=4,使|AB|=λ|AF||BF|恒成立.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题、弦长公式、一元二次方程的根与系数的关系,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
11.一个几何体的三视图如图所示,则此几何体的体积为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
4.某地区对高一年级学生的瞬时记忆能力进行调查,瞬时记忆能力包括听觉记忆能力与视觉记忆能力.现随机抽取某学校高一学生共40人,下表为该批学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为$\frac{2}{5}$.
(1)试确定a、b的值;
(2)将抽取所得学生的频率视为概率,从该地区高二年级学生中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为ξ,求随机变量ξ的分布列与数学期望Eξ及方差Dξ.
| 视觉 听觉 | 视觉记忆能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 听觉 记忆 能力 | 偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 | b | |
| 偏高 | 2 | a | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
(1)试确定a、b的值;
(2)将抽取所得学生的频率视为概率,从该地区高二年级学生中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为ξ,求随机变量ξ的分布列与数学期望Eξ及方差Dξ.
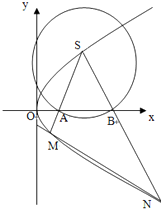 已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.
已知点F是抛物线C:y2=x的焦点,点S是抛物线C上在第一象限内的一点,且|SF|=$\frac{5}{4}$.