题目内容
18.设f(x)=x3-$\frac{1}{2}$x2-2x+5.求函数f(x)的单调递增、单调递减区间.分析 求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可.
解答 解:f′(x)=3x2-x-2=(3x+2)(x-1).
令f′(x)>0,得x<-$\frac{2}{3}$或x>1.
令f′(x)<0,得-$\frac{2}{3}$<x<1.
∴函数f(x)的单调递增区间为(-∞,-$\frac{2}{3}$),(1,+∞);单调递减区间为(-$\frac{2}{3}$,1).
点评 本题考查了函数的单调性问题,考查导数的应用,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一个红色的棱长是3cm的正方体,将其适当分割成棱长为1cm的小正方体,则三面涂色的小正方体有( )
| A. | 6个 | B. | 8个 | C. | 16个 | D. | 27个 |
 已知正方形ADEF所在平面与等腰梯形BCEF所在平面互相垂直,且BC=2BF=2EF=4,G为BC中点.
已知正方形ADEF所在平面与等腰梯形BCEF所在平面互相垂直,且BC=2BF=2EF=4,G为BC中点.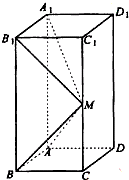 如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M是棱CC1的中点,