题目内容
11．一个几何体的三视图如图所示，则此几何体的体积为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 由已知中的三视图，可得该几何体是一个以俯视图为底面的四棱锥，代入锥体体积公式，可得答案．
解答 解：由已知中的三视图，可得该几何体是一个以俯视图为底面的四棱锥，
底面是对角线长为2的正方形，故面积S=$\frac{1}{2}$×2×2=2，
高h=$\sqrt{{\sqrt{13}}^{2}-{2}^{2}}$=3，
故体积V=$\frac{1}{3}Sh$=2，
故选：B
点评 本题考查的知识点是棱锥的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
2．某几何体的三视图如图所示，则该几何体的表面积为（ ）
| A． | 12+4$\sqrt{3}$ | B． | 12 | C． | $8+2\sqrt{3}$ | D． | 8 |
已知正方形ADEF所在平面与等腰梯形BCEF所在平面互相垂直，且BC=2BF=2EF=4，G为BC中点．
3．
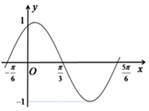如图是函数y=Asin（ωx+φ）（x∈R）在区间[-$\frac{π}{6}$，$\frac{5π}{6}$]上的图象．为了得到这个函数的图象，只需将y=sinx（x∈R）的图象上所有的点（ ）
如图是函数y=Asin（ωx+φ）（x∈R）在区间[-$\frac{π}{6}$，$\frac{5π}{6}$]上的图象．为了得到这个函数的图象，只需将y=sinx（x∈R）的图象上所有的点（ ）| A． | 向左平移$\frac{π}{3}$个单位，再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍 | |
| B． | 向左平移$\frac{π}{3}$个单位，再把所得各点的横坐标伸长到原来的2倍 | |
| C． | 向左平移$\frac{π}{6}$个单位，再把所得各点的横坐标缩短到原来的$\frac{1}{2}$倍 | |
| D． | 向左平移$\frac{π}{6}$个单位，再把所得各点的横坐标伸长到原来的2倍 |