题目内容
17.设不等式(x-a)(x+a-2)<0的解集为N,若x∈N是$x∈M=[{-\frac{1}{2},2})$的必要条件,则a的取值范围为$a≤-\frac{1}{2}或a≥\frac{5}{2}$.分析 根据充分条件和必要条件的定义,结合一元二次不等式的解法建立不等式关系进行求解即可.
解答 解:若x∈N是$x∈M=[{-\frac{1}{2},2})$的必要条件,
则M⊆N,
若a=1时,不等式(x-a)(x+a-2)<0的解集N=∅,此时不满足条件.
若a<1,则N=(a,2-a),则满足$\left\{\begin{array}{l}{a<1}\\{2-a≥2}\\{a≤-\frac{1}{2}}\end{array}\right.$,得$\left\{\begin{array}{l}{a<1}\\{a≤0}\\{a≤-\frac{1}{2}}\end{array}\right.$,此时a≤-$\frac{1}{2}$,
若a>1,则N=(2-a,a),则满足$\left\{\begin{array}{l}{a>1}\\{a≥2}\\{2-a≤-\frac{1}{2}}\end{array}\right.$,得$\left\{\begin{array}{l}{a>1}\\{a≥2}\\{a≥\frac{5}{2}}\end{array}\right.$,此时a≥$\frac{5}{2}$,
综上$a≤-\frac{1}{2}或a≥\frac{5}{2}$,
故答案为:$a≤-\frac{1}{2}或a≥\frac{5}{2}$
点评 本题主要考查充分条件和必要条件的应用,结合一元二次不等式的解法是解决本题的关键.注意要对a进行分类讨论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.将号码分别为1、2、3、4的四个小球放入一个袋中,这些小球仅号码不同,其余完全相同.甲从袋中摸出一个球,号码为a,放回后,乙从此袋再摸出一个球,其号码为b,则使不等式a>2b-2成立的事件发生的概率等于( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
12.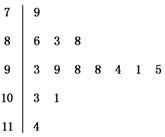 如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
 如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )
如图是某高二学生自高一至今月考从第1次到14次的数学考试成绩茎叶图,根据茎叶图计算数据的中位数为( )| A. | 98 | B. | 94 | C. | 94.5 | D. | 95 |
6.已知椭圆C:$\frac{x^2}{25}+\frac{y^2}{b^2}=1({0<b<5})$的长轴长、短轴长、焦距成等差数列,则该椭圆的方程是( )
| A. | $\frac{x^2}{25}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{25}+{y^2}=1$ |
7.已知函数f(x)=3x2-2ax-8在(1,2)上不单调,则实数a的取值范围是( )
| A. | [3,6] | B. | (-∞,3]∪[6,+∞) | C. | [3,6) | D. | (3,6) |
 试写出函数f(x)=x${\;}^{\frac{1}{2}}$的性质,并作出它的大致图象.
试写出函数f(x)=x${\;}^{\frac{1}{2}}$的性质,并作出它的大致图象.