题目内容
8.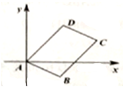 如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.
如图,面积为8的平行四边形ABCD,A为坐标原点,B坐标为(2,-1),C、D均在第一象限.(I)求直线CD的方程;
(II)若|BC|=$\sqrt{13}$,求点D的横坐标.
分析 (I)由题意,kAB=kCD=-$\frac{1}{2}$,直线CD的方程为y=-$\frac{1}{2}$x+m,即x+2y-2m=0,利用S=8,|AB|=$\sqrt{5}$,即可求直线CD的方程;
(II)若|BC|=$\sqrt{13}$,则|AD|=$\sqrt{13}$,可得$\left\{\begin{array}{l}{a+2b-8=0}\\{\sqrt{{a}^{2}+{b}^{2}}=\sqrt{13}}\end{array}\right.$,即可求点D的横坐标.
解答 解:(I)由题意,kAB=kCD=-$\frac{1}{2}$,
∴直线CD的方程为y=-$\frac{1}{2}$x+m,即x+2y-2m=0,
∵S=8,|AB|=$\sqrt{5}$,
∴$\frac{|2m|}{\sqrt{1+4}}$=$\frac{8}{\sqrt{5}}$,
∴m=±4,
由图可知m>0,∴直线CD的方程为y=-$\frac{1}{2}$x+m,即x+2y-8=0;
(II)设D(a,b),若|BC|=$\sqrt{13}$,则|AD|=$\sqrt{13}$,
∴$\left\{\begin{array}{l}{a+2b-8=0}\\{\sqrt{{a}^{2}+{b}^{2}}=\sqrt{13}}\end{array}\right.$,∴点D的横坐标a=1.2或2.
点评 本题考查直线方程,考查距离公式的运用,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16.如图,网络纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )
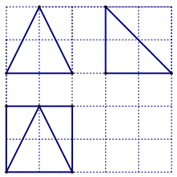

| A. | 8 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
3.在△ABC中,$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{DC}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,且则$\overrightarrow{AD}$=( )
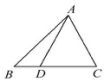

| A. | $\frac{4}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$ | B. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$ | C. | $\frac{1}{3}$$\overrightarrow{a}$-$\frac{4}{3}$$\overrightarrow{b}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ |
8.将号码分别为1、2、3、4的四个小球放入一个袋中,这些小球仅号码不同,其余完全相同.甲从袋中摸出一个球,号码为a,放回后,乙从此袋再摸出一个球,其号码为b,则使不等式a>2b-2成立的事件发生的概率等于( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |