题目内容
18．已知点A（4，0），抛物线C：x2=8y的焦点为F，射线FA与抛物线和它的准线分别交于点M和N，则|FM|：|MN|=1：$\sqrt{5}$．分析 如图所示，由抛物线定义知|MF|=|MH|，得到|FM|：|MN|=|MH|：|MN|，根据△MHN∽△FOA，即可求出答案．
解答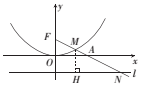 
解：如图所示，由抛物线定义知|MF|=|MH|，
所以|FM|：|MN|=|MH|：|MN|．
由于△MHN∽△FOA，
则$\frac{|MH|}{|HN|}$=$\frac{|OF|}{|OA|}$=$\frac{2}{4}$=$\frac{1}{2}$，
则|MH|：|MN|=1：$\sqrt{5}$，
即|FM|：|MN|=1：$\sqrt{5}$．
故答案为：1：$\sqrt{5}$
点评 本题给出抛物线方程和射线FA，求线段的比值、抛物线的定义、标准方程和简单几何性质等知识，属于中档题．
练习册系列答案
相关题目
8．将号码分别为1、2、3、4的四个小球放入一个袋中，这些小球仅号码不同，其余完全相同．甲从袋中摸出一个球，号码为a，放回后，乙从此袋再摸出一个球，其号码为b，则使不等式a＞2b-2成立的事件发生的概率等于（ ）
| A． | $\frac{3}{8}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
试写出函数f（x）=x${\;}^{\frac{1}{2}}$的性质，并作出它的大致图象．
6．已知椭圆C：$\frac{x^2}{25}+\frac{y^2}{b^2}=1（{0＜b＜5}）$的长轴长、短轴长、焦距成等差数列，则该椭圆的方程是（ ）
| A． | $\frac{x^2}{25}+\frac{y^2}{4}=1$ | B． | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | C． | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D． | $\frac{x^2}{25}+{y^2}=1$ |
13．函数f（x）=x+cosx在[0，π]上的最小值为（ ）
| A． | -2 | B． | 0 | C． | -$\frac{1}{2}$ | D． | 1 |
3．已知$α∈（{\frac{π}{2}，\frac{3π}{2}}），tan（{α-π}）=-\frac{3}{4}$，则sinα+cosα的值是（ ）
| A． | $±\frac{1}{5}$ | B． | $\frac{1}{5}$ | C． | $-\frac{1}{5}$ | D． | $-\frac{7}{5}$ |
7．已知函数f（x）=3x2-2ax-8在（1，2）上不单调，则实数a的取值范围是（ ）
| A． | [3，6] | B． | （-∞，3]∪[6，+∞） | C． | [3，6） | D． | （3，6） |