题目内容
16.已知等比数列{an}中,a1=2,a3+2是a2和a4的等差中项.(1)求数列{an}的通项公式;
(2)记bn=nan,求数列{bn}的前n项sn.
分析 (1)等比数列{an}中,a1=2,a3+2是a2和a4的等差中项,有等比数列的首项和公比分别表示出已知条件,解方程组即可求得首项和公比,代入等比数列的通项公式即可求得结果;
(2)把(1)中求得的结果代入bn=nan,求出bn,利用错位相减法求出Tn.
解答 解:(1)设数列{an}的公比为q,
由题意知:2(a3+2)=a2+a4,
∴q3-2q2+q-2=0,即(q-2)(q2+1)=0.
∴q=2,即an=2•2n-1=2n.
(2)bn=n•2n,
∴Sn=1•2+2•22+3•23+…+n•2n.①
2Sn=1•22+2•23+3•24+…+(n-1)•2n+n•2n+1.②
①-②得-Sn=21+22+23+24+…+2n-n•2n+1
=-2-(n-1)•2n+1.
∴Sn=2+(n-1)•2n+1.
点评 考查等比数列求通项公式和等差、等比中项的概念及错位相减法求数列的前项和Sn,等差数列和等比数列之间的相互转化,考查运算能力,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.如图,网络纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的体积为( )
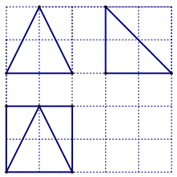

| A. | 8 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
8.将号码分别为1、2、3、4的四个小球放入一个袋中,这些小球仅号码不同,其余完全相同.甲从袋中摸出一个球,号码为a,放回后,乙从此袋再摸出一个球,其号码为b,则使不等式a>2b-2成立的事件发生的概率等于( )
| A. | $\frac{3}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
6.已知椭圆C:$\frac{x^2}{25}+\frac{y^2}{b^2}=1({0<b<5})$的长轴长、短轴长、焦距成等差数列,则该椭圆的方程是( )
| A. | $\frac{x^2}{25}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{25}+{y^2}=1$ |