题目内容

8．设函数$f（x）=lnx+\frac{1}{x}$，则函数y=f（x）的单调递增区间是（1，+∞）．

分析 求出函数的导数，解关于导函数的不等式，求出函数的单调区间即可．

解答 解：∵$f（x）=lnx+\frac{1}{x}$，（x＞0），
∴f′（x）=$\frac{1}{x}$-$\frac{1}{{x}^{2}}$=$\frac{x-1}{{x}^{2}}$，
令f′（x）＞0，解得：x＞1，
故函数的递增区间是（1，+∞），
故答案为：（1，+∞）．

点评 本题考查了函数的单调性问题，考查导数的应用，是一道基础题．

练习册系列答案
相关题目
18．如图，在平行六面体ABCD-A1B1C1D1中，底面是边长为2的正方形，若$∠{A_1}AB=∠{A_1}AD={60^0}$，且A1A=3，则A1C的长为$\sqrt{17}$．
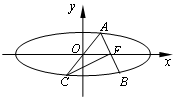19．如图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的右焦点为F，过F的直线交椭圆于A，B两点，点C是点A关于原点O的对称点，若CF⊥AB且CF=AB，则椭圆的离心率为$\sqrt{6}-\sqrt{3}$．
16．已知集合A={x|log2x＞m}，B={x|-4＜x-4＜4}．
（1）当m=2时，求A∪B，A∩B；
（2）若A⊆∁RB，求实数m的取值范围．
3．设数列{an}满足：a1=1，3a2-a1=1，且$\frac{2}{{a}_{n}}$=$\frac{{a}_{n-1}+{a}_{n+1}}{{a}_{n-1}{a}_{n+1}}$（n≥2）
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列b1=$\frac{1}{2}$，4bn=an-1an，设{bn}的前n项和Tn．证明：Tn＜1．
13．已知函数f（x）=2cosxsin（x+$\frac{π}{3}$）-$\frac{\sqrt{3}}{2}$．
（Ⅰ）求函数f（x）的最小正周期和对称中心；
（Ⅱ）求函数f（x）在区间[$\frac{π}{3}$，π]上的取值范围．
2．已知A=$（\begin{array}{l}{0}&{1}&{0}\\{0}&{0}&{1}\\{1}&{0}&{0}\end{array}）$．
（1）求A2，A3，A2014．
（2）若n阶方阵B=$[\begin{array}{l}{0}&{1}&{0}&{0}&{…}&{0}\\{0}&{0}&{1}&{0}&{…}&{0}\\{0}&{0}&{0}&{1}&{…}&{0}\\{…}&{…}&{…}&{…}&{…}&{…}\\{0}&{0}&{0}&{0}&{…}&{1}\\{1}&{0}&{0}&{0}&{…}&{0}\end{array}]$（左下角1的余子式为n-1阶单位矩阵），试求出Bk（k∈N*）．
（3）若C=$（\begin{array}{l}{{c}_{0}}&{{c}_{1}}&{{c}_{2}}\\{{c}_{2}}&{{c}_{0}}&{{c}_{1}}\\{{c}_{1}}&{{c}_{2}}&{{c}_{0}}\end{array}）$，则称此矩阵为三阶循环矩阵，请你参考（1）的计算过程证明两个三阶循环矩阵的乘积仍为三阶循环矩阵．三阶循环矩阵的乘法是否满足交换律？如果是，请说明理由，如果不是，请举出反例．
19．在极坐标系中，点（2，$\frac{2π}{3}$）到直线$ρsin（θ-\frac{π}{3}）$=0的距离为（　　）
A．$\sqrt{2}$B．2C．$\sqrt{3}$D．3
20．已知函数$f（x）=\sqrt{（{{a^2}-1}）{x^2}-（{a-1}）x+1}$的定义域是全体实数，那么实数a的取值范围是（-∞，-$\frac{5}{3}$]∪[1，+∞）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网