题目内容
16.已知集合A={x|log2x>m},B={x|-4<x-4<4}.(1)当m=2时,求A∪B,A∩B;
(2)若A⊆∁RB,求实数m的取值范围.
分析 (1)当m=2时,求出集合A,B,即可求A∪B,A∩B;
(2)A={x|log2x>m}={x|x>2m},∁RB={x|x≤0或x≥8},利用A⊆∁RB,求实数m的取值范围.
解答 解:(1)当m=2时,A={x|log2x>m}={x|x>4},
B={x|-4<x-4<4}={x|0<x<8}.
∴A∪B={x|x>0},A∩B={x|4<x<8};
(2)A={x|log2x>m}={x|x>2m},∁RB={x|x≤0或x≥8}
若A⊆∁RB,则2m>8,∴m≥3.
点评 本题考查集合的运算,考查学生解不等式的能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
8.$y=3sin(\frac{x}{2}-\frac{π}{3})$的一条对称轴是( )
| A. | $x=\frac{2π}{3}$ | B. | $x=\frac{π}{2}$ | C. | $x=-\frac{π}{3}$ | D. | $x=\frac{8π}{3}$ |
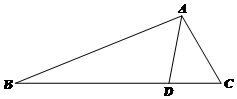 如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.
如图,在△ABC中,D是BC上的点,AC=3,CD=2,AD=$\sqrt{7}$,sinB=$\frac{\sqrt{7}}{7}$.