题目内容
9.已知函数f(x)=|x-a|(a>0).(Ⅰ)求证:f(m)+f(n)>|m-n|;
(Ⅱ)解不等式f(x)+f(-x)>2.
分析 (Ⅰ)根据|a+b|≤|a|+|b|,可得|m-a|+|a-n|≥|m-a+a-n|=|m-n|,即可证明:f(m)+f(n)>|m-n|;
(Ⅱ)分类讨论,去掉绝对值符号,即可解不等式f(x)+f(-x)>2.
解答 (Ⅰ)证明:f(m)+f(n)=|m-a|+|n-a|=|m-a|+|a-n|,
根据|a+b|≤|a|+|b|,∴|m-a|+|a-n|≥|m-a+a-n|=|m-n|
即f(m)+f(n)≥|m-n|; …(5分)
(Ⅱ)解:由f(x)+f(-x)>2,即|x-a|+|x+a|≥2,
(ⅰ)若0<a≤1时,
当-a≤x≤a时,不等式即a-x+x+a>2,即a>1,原不等式不成立
当x>a时,原不等式即x-a+x+a>2,x>1
当x<-a时,原不等式即a-x-x-a>2,解得x<-1
∴0<a≤1时,原不等式解集为(-∞,-1)U(1,+∞);
(ⅱ)若a>1
当-a≤x≤a时,不等式即a-x+x+a>2,2a>2恒成立,原不等式,解得-a≤x≤a
当x>a时,原不等式即x-a+x+a>2,x>1与x>a取交集得x>a
当x<-a时,原不等式即a-x-x-a>2,解得x<-1与x<-a取交集得x<-a
∴a>1时,原不等式解集.…(10分)
点评 本题考查绝对值不等式的解法,通过对x范围的分析讨论,去掉绝对值符号,利用一次函数的单调性求最值是关键,考查运算与推理证明的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知全集U={x∈N+|-2<x<9},M=(3,4,5),P={1,3,6},那么{2,7,8}是( )
| A. | M∪P | B. | M∩P | C. | (∁UM)∪(∁∪P) | D. | (∁UM)∩(∁UP) |
20.下列函数在(0,+∞)上为减函数的是( )
| A. | y=-|x-1| | B. | y=x2-2x+3 | C. | y=ln(x+1) | D. | y=2${\;}^{-\frac{x}{2}}$ |
14.如图是一个三棱柱的正视图和俯视图,其俯视图是面积为8$\sqrt{2}$的矩形,则该三棱柱的体积是( )
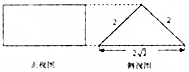

| A. | 8 | B. | 4$\sqrt{2}$ | C. | 16 | D. | $\frac{16}{3}$ |
18.从1,2,3,4,5中任意取出两个不同的数,则这两个数不相邻的概率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |