题目内容
设
，
，
为同一平面内具有相同起点的任意三个非零向量，且满足
与
不共线，
⊥
，|
|=|
|，则|
•
|的值一定等于（ ）
| x1 |
| x2 |
| x3 |
| x1 |
| x2 |
| x1 |
| x3 |
| x1 |
| x3 |
| x2 |
| x3 |
A、以
| ||||
B、以
| ||||
C、以
| ||||
D、以
|
考点：平面向量数量积的运算,向量的模
专题：计算题,平面向量及应用
分析：由题意可以画出图形：记
=
，
=
，
=
，由于这三向量的起点相同，且满足
与
不共线，
⊥
，|
|=|
|，利用向量的内积及图形可以求得．
| OA |
| x1 |
| OB |
| x2 |
| OC |
| x3 |
| x1 |
| x2 |
| x1 |
| x3 |
| x1 |
| x3 |
解答：
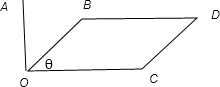解：由题意可以画出图形：
记
=
，
=
，
=
，记＜
，
＞=θ
因为这三向量的起点相同，且满足
与
不共线，
⊥
，|
|=|
|，利用向量的内积定义，所以|
•
|=||OB||OC|
cosθ|，
又由于S△BOC=
|OB||OC|sinθ，所以||OB||OC|sinθ|=S四边形OBDC．
故选B．
解：由题意可以画出图形：记
| OA |
| x1 |
| OB |
| x2 |
| OC |
| x3 |
| x2 |
| x3 |
因为这三向量的起点相同，且满足
| x1 |
| x2 |
| x1 |
| x3 |
| x1 |
| x3 |
| x2 |
| x3 |
cosθ|，
又由于S△BOC=
| 1 |
| 2 |
故选B．
点评：此题考查了利用图形分析题意的数形结合的能力，向量的内积，三角形的面积公式．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
已知正方体ABCD-A1B1C1D1，过顶点A1作平面α，使得直线AC和BC1平面α所成的角都为30°，这样的平面α可以有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
若a=log23，b=log32，c=esinπ，则a，b，c 的大小关系为（ ）
| A、a＜b＜c |
| B、c＜b＜a |
| C、a＜c＜b |
| D、b＜c＜a |
