题目内容
18.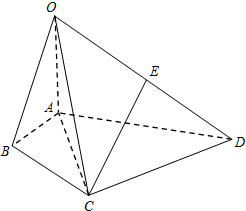 如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.
如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.(1)求证:CE∥平面OAB;
(2)求四面体OACE的体积.
分析 (1)证明平面CEF∥平面OAB,即可证明CE∥平面OAB;
(2)求出E到平面OAC的距离为h=$\frac{1}{2}CD$=$\sqrt{3}$,即可求四面体OACE的体积.
解答  (1)证明:取AD中点F,连接EF,CF,则EF∥OA,
(1)证明:取AD中点F,连接EF,CF,则EF∥OA,
∵EF?平面OAB,OA?平面OAB,
∴EF∥平面OAB,
△ACF中,AC=AF,∠CAF=60°,∴∠ACF=60°,
∵∠BAC=60°,
∴AB∥CF,
∵CF?平面OAB,AB?平面OAB,
∴CF∥平面OAB,
∵EF∩CF=F,
∴平面CEF∥平面OAB,
∵CE?平面CEF,
∴CE∥平面OAB;
(2)解:在△ACD中,CD=$\sqrt{A{C}^{2}+A{D}^{2}-2AC•AD•cos∠CAD}$=2$\sqrt{3}$,
∴AC2+CD2=AD2,
∴AC⊥CD,
∵OA⊥平面ABCD,CD?平面ABCD,
∴OA⊥CD,
∵AC∩OA=A,
∴CD⊥平面OAC,
∵E是OD的中点,
∴E到平面OAC的距离为h=$\frac{1}{2}CD$=$\sqrt{3}$,
∵S△OAC=$\frac{1}{2}×2×2$=2,
∴四面体OACE的体积V=$\frac{1}{3}×2×\sqrt{3}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查线面平行,考查体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
12.Rt△ABC中,斜边BC为4,以BC中点为圆心,作半径为1的圆,分别交BC于P、Q两点,则|AP|2+|AQ|2+|PQ|2的值为( )
| A. | 4+$\sqrt{17}$ | B. | 3+$2\sqrt{5}$ | C. | $\frac{19}{2}$ | D. | 14 |
 是非零向量且满足
是非零向量且满足 则
则 的夹角是( )
的夹角是( )  B.
B. C.
C. D.
D.
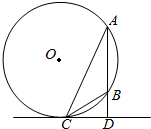 如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1
如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1 已知,如图正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB,AD的中点.
已知,如图正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB,AD的中点.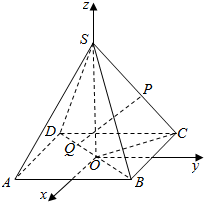 在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.
在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.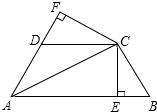 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.