题目内容
12.Rt△ABC中,斜边BC为4,以BC中点为圆心,作半径为1的圆,分别交BC于P、Q两点,则|AP|2+|AQ|2+|PQ|2的值为( )| A. | 4+$\sqrt{17}$ | B. | 3+$2\sqrt{5}$ | C. | $\frac{19}{2}$ | D. | 14 |
分析 利用余弦定理,求出|AP|2、|AQ|2,结合∠AOP+∠AOQ=180°,即可求|AP|2+|AQ|2+|PQ|2的值.
解答 解:由题意,OA=OB=2,OP=OQ=1
△AOP中,根据余弦定理AP2=OA2+OP2-2OA•OPcos∠AOP
同理△AOQ中,AQ2=OA2+OQ2-2OA•OQcos∠AOQ
因为∠AOP+∠AOQ=180°,
所以|AP|2+|AQ|2+|PQ|2=2OA2+2OP2+PQ2=2×22+2×12+(2×1)2=14.
故选:D.
点评 本题考查直线与圆的位置关系的应用,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目
19.已知A(2,-5,1),B(1,-4,1),C(2,-2,4),则$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
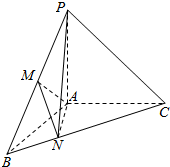 如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.
如图,在三棱锥P-ABC中,PA⊥面ABC,∠BAC=120°,且AB=AC=AP=1,M为PB的中点,N在BC上,且AN=BN.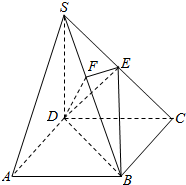 如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.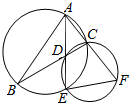 如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.
如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D,E,C三点的圆于点F.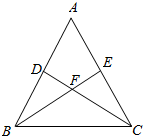 如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.
如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.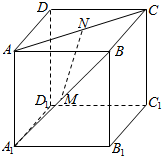 如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是棱A1B、AC上的点,A1M=AN.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是棱A1B、AC上的点,A1M=AN.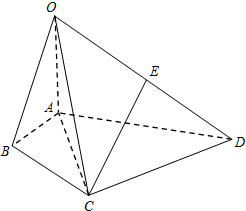 如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.
如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.