题目内容
7.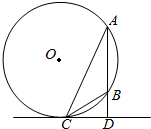 如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1
如图,A、B是圆O上的两点,且AB的长度小于圆O的直径,直线l与AB垂于点D且与圆O相切于点C.若AB=2,DB=1(1)求证:CB为∠ACD的角平分线;
(2)求圆O的直径的长度.
分析 (1)由切割线定理得CD2=DA•DB=3,证明∠ACB=∠CAB,利用CD为圆O的切线,∠BCD=∠,可得∠BCD=∠ACB,即可证明CB为∠ACD的角平分线;
(2)连结AO并延长交圆O于点E,连结CE,求出AE,即可求圆O的直径的长度.
解答  (1)证明:由切割线定理得CD2=DA•DB=3,
(1)证明:由切割线定理得CD2=DA•DB=3,
∴$CD=\sqrt{3}$…(1分)
又∵在Rt△CDB中,CB2=CD2+BD2=3+1=4…(2分)
∴在Rt△CBA中,CB=AB=2,
∴∠ACB=∠CAB…(3分)
又∵CD为圆O的切线,
∴∠BCD=∠CAB…(4分)
∴∠BCD=∠ACB,CB为∠ACD的角平分线 …(5分)
(2)解:连结AO并延长交圆O于点E,连结CE,
设DC延长线上一点为F,则
∵AE为圆O直径,∴$∠ACE=\frac{π}{2}$
∵直线l与圆O相切于点C.∴∠ACD=∠E,∠BCD=∠2,
∴∠1=∠2(等角的余角相等)
∴∠1=∠2=∠BCD=∠ACB…(6分)
∴EC=BC=AB=2(相等的圆周角所对的弦相等) …(7分)
∵AC2=AD2+CD2=9+3=12…(8分)
∴AE2=EC2+AC2=4+12=16…(9分)
∴AE=4圆O的直径为4 …(10分)
点评 本题考查切割线定理,圆的切线的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
11.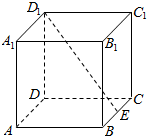 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为( )| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | 2 | C. | $2\sqrt{2}$ | D. | 3 |
 ,应用秦九韶算法计算
,应用秦九韶算法计算 时的值时,
时的值时, =_____
=_____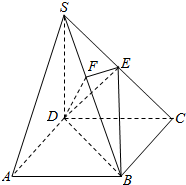 如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.
如图,在四棱锥S-ABCD中,底面ABCD是矩形,SD=DC=2AD,侧棱SD⊥底面ABCD,点E是SC的中点,点F在SB上,且EF⊥SB.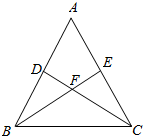 如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.
如图,在△ABC中,DC⊥AB于D,BE⊥AC于E,BE交DC于点F,若BF=FC=3,DF=FE=2.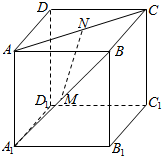 如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是棱A1B、AC上的点,A1M=AN.
如图所示,在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是棱A1B、AC上的点,A1M=AN.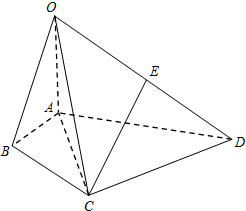 如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.
如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.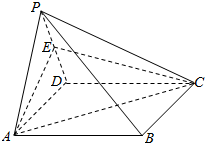 已知四棱锥P-ABCD的底面ABCD是矩形,PD⊥底面ABCD,E为棱PD的中点.
已知四棱锥P-ABCD的底面ABCD是矩形,PD⊥底面ABCD,E为棱PD的中点.