题目内容
8.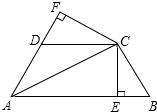 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.(1)求证:△CFD≌△CEB;
(2)若AB=21,AD=9.求AE的长.
分析 (1)利用HL,证明:△CFD≌△CEB;
(2)若AB=21,AD=9.求出EB=DF=4,即可求AE的长.
解答 (1)证明:∵AC平分∠BAD,CE⊥AB于E,CF⊥AD于F
∴CE=CF,
在Rt△BCE和Rt△DCF中,
∵CE=CF,BC=CD,
∴△CFD≌△CEB (HL).(3分)
(2)解:∵Rt△BCE≌Rt△DCF,
∴DF=EB,CE=CF,CE⊥AB于E,CF⊥AD于F,
∴Rt△ACE≌Rt△ACF,
∴AF=AE,(2分)
∵AB=15,AD=7,
∴AD+DF=AB-EB,
∴EB=DF=4,(2分)
∴AE=AF=AD+DF=11.
点评 本题考查三角形全等的证明,考查学生的计算能力,正确证明三角形全等是关键.

练习册系列答案
相关题目
19.已知A(2,-5,1),B(1,-4,1),C(2,-2,4),则$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
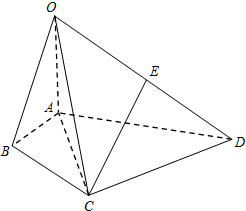 如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.
如图,在四棱锥O-ABCD中,∠BAD=120°,OA⊥平面ABCD,E为OD的中点,OA=AC=$\frac{1}{2}$AD=2,AC平分∠BAD.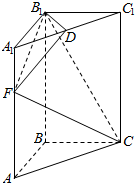 如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1.
如图,高为3的直三棱柱ABC-A1B1C1中,底面是直角三角形,AC=2,D为A1C1的中点,F在线段AA1上,CF⊥DB1,且A1F=1. 的图象向右平移
的图象向右平移 个单位后与
个单位后与 的图象重合,则
的图象重合,则 _________.
_________.