题目内容
已知函数f（x）=（sinx+cosx）2+2cos2x
（1）求f（x）的最小正周期及最大值；
（2）求f（x）的单调减区间．
（1）求f（x）的最小正周期及最大值；
（2）求f（x）的单调减区间．
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：（1）根据二倍角的正弦与余弦及辅助角公式，将解析式化为y=Asin（ωx+φ）+B的基本形式，根据正弦函数的性质，求出最小正周期和最大值；
（2）根据正弦函数的单调减区间，并把“2x+
”当做一个整体求出x的范围，即求出函数的减区间．
（2）根据正弦函数的单调减区间，并把“2x+
| π |
| 4 |
解答：
解：（1）由题意得，
f（x）=（sinx+cosx）2+2cos2x
=1+2sinxcosx+1+cos2x
=sin2x+cos2x+2
=
sin(2x+
)+2，
∴它的最小正周期T=π，f（x）最大值是
+2；
（2）由（1）得，f（x）=
sin(2x+
)+2
由
+2kπ≤2x+
≤
+2kπ（k∈Z）得，
+kπ≤x≤
+kπ（k∈Z）
所以f（x）的递减区间为[
+kπ，
+kπ]（k∈Z）
f（x）=（sinx+cosx）2+2cos2x
=1+2sinxcosx+1+cos2x
=sin2x+cos2x+2
=
| 2 |
| π |
| 4 |
∴它的最小正周期T=π，f（x）最大值是
| 2 |
（2）由（1）得，f（x）=
| 2 |
| π |
| 4 |
由
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
所以f（x）的递减区间为[
| π |
| 8 |
| 5π |
| 8 |
点评：本题考查了二倍角的正弦与余弦、辅助角公式的应用，考查了正弦函数的周期性、最值和单调性，属于中档题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
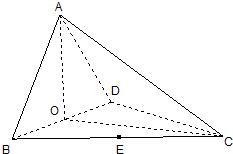如图，四面体ABCD中，O、E分别是BD、BC的中点，AB=AD=
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x（吨）与相应的生产能耗y（吨标准煤）的几组对照数据．