题目内容
若双曲线C的离心率为2,其中一个焦点F(2,0)
(1)求双曲线C的标准方程;
(2)若直线l斜率为2且过点F,求直线l被双曲线C截得的弦长.
(1)求双曲线C的标准方程;
(2)若直线l斜率为2且过点F,求直线l被双曲线C截得的弦长.
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由已知条件列出方程求出a,利用双曲线的三参数的关系,求出b,据双曲线焦点的位置求出双曲线的标准方程;
(2)直线方程为y=2x-4代入x2-
=1,整理,利用弦长公式,可求直线l被双曲线C截得的弦长.
(2)直线方程为y=2x-4代入x2-
| y2 |
| 3 |
解答:
解:∵离心率等于2,一个焦点的坐标为(2,0),
∴
=2,c=2且焦点在x轴上,
∴a=1
∵c2=a2+b2
∴b2=3
∴双曲线C的标准方程为x2-
=1;
(2)直线方程为y=2x-4代入x2-
=1,整理可得x2-16x+19=0,
∴直线l被双曲线C截得的弦长为
•
=30.
∴
| c |
| a |
∴a=1
∵c2=a2+b2
∴b2=3
∴双曲线C的标准方程为x2-
| y2 |
| 3 |
(2)直线方程为y=2x-4代入x2-
| y2 |
| 3 |
∴直线l被双曲线C截得的弦长为
| 1+4 |
| 162-4•19 |
点评:求圆锥曲线的方程关键先判断出焦点的位置、考查双曲线中三参数的关系为c2=a2+b2,注意与椭圆中三个参数关系的区别.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
已知集合A={x|x=
+
π,k∈Z},B={x|x=
+
π,k∈Z},则( )
| kπ |
| 2 |
| 1 |
| 4 |
| kπ |
| 4 |
| 1 |
| 2 |
| A、A=B | B、A?B |
| C、A?B | D、A∩B=∅ |
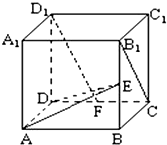 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.