题目内容
已知函数f(x)=2alnx-x+
,(a∈R,且a≠0);g(x)=-x2-x+2
b.
(Ⅰ)若f(x)在定义域上有极值,求实数a的取值范围;
(Ⅱ)若对?x1∈[1,e],总?x2∈[1,e],使得f(x1)<g(x2),则等价为fmax(x)<gmax(x),利用导数与最值之间的关系,即可求实数b的取值范围.
(Ⅲ)对?n∈N,且n≥2,证明:ln(n!)4<(n-1)(n+2).
| 1 |
| x |
| 2 |
(Ⅰ)若f(x)在定义域上有极值,求实数a的取值范围;
(Ⅱ)若对?x1∈[1,e],总?x2∈[1,e],使得f(x1)<g(x2),则等价为fmax(x)<gmax(x),利用导数与最值之间的关系,即可求实数b的取值范围.
(Ⅲ)对?n∈N,且n≥2,证明:ln(n!)4<(n-1)(n+2).
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,根据f(x)在定义域上有极值,建立导数之间的关系,即可求实数a的取值范围;
(Ⅱ)当a=
时,若对?x1∈[1,e],总?x2∈[1,e],使得f(x1)<g(x2),求实数b的取值范围.
(Ⅲ)根据导数,判断函数的单调性,利用单调性即可证明不等式.
(Ⅱ)当a=
| 2 |
(Ⅲ)根据导数,判断函数的单调性,利用单调性即可证明不等式.
解答:
解:(Ⅰ)f(x)的定义域为(0,+∞),要f(x)在定义域内有极值,
则f′(x)=
=0?-x2+2ax-1=0有两不等正根,
∴
⇒a>1.
(Ⅱ)f(x)=2
lnx-x+
,要对?x1∈[1,e],总?x2∈[1,e],使得f(x1)<g(x2)
则只需fmax(x)<gmax(x),
由f′(x)=
>0⇒
-1<x<
+1,
得函数f(x)在(1,
+1)上递增,在(
+1,e)上递减,
∴函数f(x)在x=25处有最大值;
则fmax(x)=f(
+1)=2
ln(
+1)-2;
又g(x)在(1,e)上递减,
故gmax(x)=g(1)=2
b-2
故有2
b-2>2
ln(
+1)-2⇒b>ln(
+1).
(Ⅲ)当a=1时,f(x)=2lnx-x+
,f′(x)=
≤0恒成立,
故f(x)在定义域(0,+∞)上单调递减,
故当x≥1时,f(x)=2lnx-x+
≤f(1)=0即2lnx≤x-
,
故对?n∈N,且n≥2,总有2lnn≤n-
<n,
故有2(ln2+ln3+…+lnn)<2+3+…+n?2ln(n!)<
?ln(n!)4<(n-1)(n+2)成立.
则f′(x)=
| -x2+2ax-1 |
| x2 |
∴
|
(Ⅱ)f(x)=2
| 2 |
| 1 |
| x |
则只需fmax(x)<gmax(x),
由f′(x)=
-x2+2
| ||
| x2 |
| 2 |
| 2 |
得函数f(x)在(1,
| 2 |
| 2 |
∴函数f(x)在x=25处有最大值;
则fmax(x)=f(
| 2 |
| 2 |
| 2 |
又g(x)在(1,e)上递减,
故gmax(x)=g(1)=2
| 2 |
故有2
| 2 |
| 2 |
| 2 |
| 2 |
(Ⅲ)当a=1时,f(x)=2lnx-x+
| 1 |
| x |
| -x2+2x-1 |
| x2 |
故f(x)在定义域(0,+∞)上单调递减,
故当x≥1时,f(x)=2lnx-x+
| 1 |
| x |
| 1 |
| x |
故对?n∈N,且n≥2,总有2lnn≤n-
| 1 |
| n |
故有2(ln2+ln3+…+lnn)<2+3+…+n?2ln(n!)<
| (n+2)(n-1) |
| 2 |
点评:本题主要考查导数的应用,利用导数求函数的最值,要求熟练掌握导数的应用和基本运算,综合性较强,难度较大.

练习册系列答案
相关题目
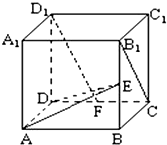 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点.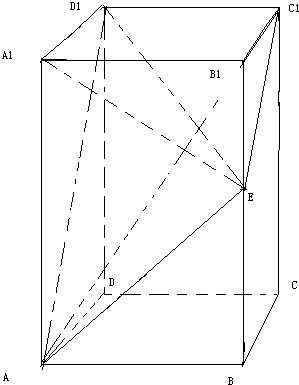 长方体ABCD-A1B1C1D1中,AB=AD=1,BB1=2,E为BB1的中点.(1)求证:AE⊥平面A1D1E;
长方体ABCD-A1B1C1D1中,AB=AD=1,BB1=2,E为BB1的中点.(1)求证:AE⊥平面A1D1E;