题目内容
点P在正方体ABCD-A1B1C1D1的底面ABCD所在平面上，E是A1A的中点，且∠EPA=∠D1PD，则点P的轨迹是（ ）
| A、直线 | B、圆 | C、抛物线 | D、双曲线 |
考点：轨迹方程
专题：计算题,直线与圆,空间角
分析：点P在正方体ABCD-A1B1C1D1的底面ABCD所在平面上，E是A1A的中点，且∠EPA=∠D1PD，可得PD=2PA，以DA所在直线为x轴，DA的垂直平分线为y轴，正方体的棱长为2a，求出方程，即可得出点P的轨迹
解答：
解：∵点P在正方体ABCD-A1B1C1D1的底面ABCD所在平面上，E是A1A的中点，且∠EPA=∠D1PD，
∴PD=2PA，
以DA所在直线为x轴，DA的垂直平分线为y轴，正方体的棱长为2a，P（x，y），则
=2
，
即3x2+3y2-10ax+3a2=0，表示圆．
故选：B．
∴PD=2PA，
以DA所在直线为x轴，DA的垂直平分线为y轴，正方体的棱长为2a，P（x，y），则
| (x+a)2+y2 |
| (x-a)2+y2 |
即3x2+3y2-10ax+3a2=0，表示圆．
故选：B．
点评：本题考查立体几何中的轨迹问题，考查学生分析解决问题的能力，正确求方程是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设F1、F2分别是双曲线
-
=1（a＞0，b＞0）的左、右焦点，如双曲线上存在点P，使得∠PF1F2=30°，∠PF2F1=120°，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）=ax-
的图象可能是（ ）
| 1 |
| a |
A、 |
B、 |
C、 |
D、 |
直线a∥平面α，则a平行于平面α内的（ ）
| A、一条确定的直线 |
| B、任意一条直线 |
| C、所有的直线 |
| D、无穷多条平行直线 |
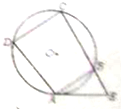如图，四边形ABCD内接于圆O，点E在CB的延长线上，AE切圆于O于点A，若AB∥CD，AD=4| 3 |
| 3 |
| A、36 | ||
| B、6 | ||
| C、24 | ||
D、2
|
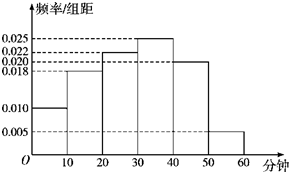我校为了了解高二级学生参加体育活动的情况，随机抽取了100名高二级学生进行调查．如图是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图．将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”．根据已知条件完成下面的列联表，并据此资料，在犯错误的概率不超过5%的前提下，你是否认为参加体育活动的“积极分子”与性别有关？