题目内容
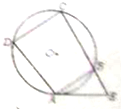如图，四边形ABCD内接于圆O，点E在CB的延长线上，AE切圆于O于点A，若AB∥CD，AD=4| 3 |
| 3 |
| A、36 | ||
| B、6 | ||
| C、24 | ||
D、2
|
考点：与圆有关的比例线段
专题：选作题,立体几何
分析：先求出BC=AD=4
，再利用切割线定理，即可得出结论．
| 3 |
解答：
解：∵AB∥CD，AD=4
，
∴BC=AD=4
，
∵AE切圆于O于点A，
∴AE2=EB•EC，
∵BE=2
，
∴AE2=2
•6
=36，
∴AE=6，
故选：B．
| 3 |
∴BC=AD=4
| 3 |
∵AE切圆于O于点A，
∴AE2=EB•EC，
∵BE=2
| 3 |
∴AE2=2
| 3 |
| 3 |
∴AE=6，
故选：B．
点评：本题考查切割线定理，考查圆的性质，考查学生的计算能力，比较基础．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
定义x?y=x3-y，则2?5等于（ ）
| A、-2 | B、0 | C、3 | D、5 |
在△ABC中，动点P满足|
|2=|
|2-2
•
，则P点的轨迹一定通过△ABC的（ ）
| CA |
| CB |
| AB |
| CP |
| A、外心 | B、内心 | C、重心 | D、垂心 |
点P在正方体ABCD-A1B1C1D1的底面ABCD所在平面上，E是A1A的中点，且∠EPA=∠D1PD，则点P的轨迹是（ ）
| A、直线 | B、圆 | C、抛物线 | D、双曲线 |
已知函数f（x）=m2-2cosx•m-sin2x在cosx=-1时取得最大值，在cosx=m时取得最小值，则实数m的取值范围为（ ）
| A、m≤-1 | B、m≥1 |
| C、0≤m≤1 | D、-1≤m≤0 |
设A，B是抛物线y2=4x上的点，且|AB|=8，则AB中点M的横坐标的最小值为（ ）
| A、4 | B、3 | C、2 | D、1 |
复数
等于（ ）
| i3 |
| 1-i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|