题目内容
7.设函数f(x)对任意实数x满足f(x)=-f(x+2),且当0≤x≤2时,f(x)=x(2-x),若关于x的方程f(x)=kx有3个不等的实数解,则k的取值范围是(10-4$\sqrt{6}$,2).分析 先确定函数f(x)为周期函数,再将问题等价方程f(x)仅有唯一实数根,并结合函数的图象与判别式得出k的取值范围.
解答 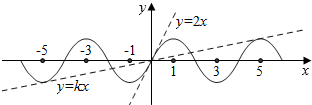 解:∵f(x)=-f(x+2),∴f(x+4)=f(x),
解:∵f(x)=-f(x+2),∴f(x+4)=f(x),
即f(x)是以4为周期的函数,
因为,当x∈[0,2]时,f(x)=x(2-x),
所以,x∈[-2,0]时,x+2∈[0,2],
所以,f(x)=-f(x+2)=x(x+2),
∴f(x)在一个周期内的解析式为f(x)=$\left\{\begin{array}{l}{x(2-x),x∈[0,2]}\\{x(2+x),x∈[-2,0)}\end{array}\right.$,如右图,
依题意,方程f(x)=kx有三个不等的实根,
则该方程一根为负,一根为正,一根为0,即f(x)=kx只有唯一一个正实数根,
当x∈[4,6]时,x-4∈[0,2],
所以,f(x)=f(x-4)=(x-4)(6-x),
令(x-4)(6-x)=kx,整理得,x2+(k-10)x+24=0,
由△=0,解得k=10-4$\sqrt{6}$(舍k=10+4$\sqrt{6}$),
此时,直线y=(10-4$\sqrt{6}$)x与f(x)的图象相切,共有5个交点,如图蓝色直线,
所以,k>10-4$\sqrt{6}$,------------------①
另一方面,函数f(x)=x(2-x)在x=0处的导数为f'(0)=2,
即直线y=2x与f(x)的图象只有一个交点,如图红色直线,
所以,k<2,------------------------②
当2<x<4时,-2<x-4<0,f(x-4)=(x-4)(x-2),可得f(x)=f(x-4)=x2-6x+8,
由x2-6x+8=kx,可得判别式为(6+k)2-32=0,
解得k=4$\sqrt{2}$-6(-4$\sqrt{2}$-6舍去),
当直线y=kx(k<0)与y=f(x)相切可得4$\sqrt{2}$-6.
综合以上讨论得,k∈(10-4$\sqrt{6}$,2).
故答案为:(10-4$\sqrt{6}$,2)∪{4$\sqrt{2}$-6}.
点评 本题主要考查了抽象函数及其应用,涉及函数周期性的判断与应用,函数的图象与性质,以及函数零点个数的判断,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
| A. | ∅ | B. | {0} | C. | {0,1} | D. | {0,1,2} |
| A. | 20 | B. | 14 | C. | 12 | D. | 10 |
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
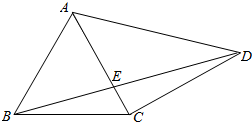 如图,△ABC是等边三角形,△ACD是等腰直角三角形,∠ACD=90°,BD交AC于E,AB=$\sqrt{2}$
如图,△ABC是等边三角形,△ACD是等腰直角三角形,∠ACD=90°,BD交AC于E,AB=$\sqrt{2}$