题目内容
9.已知△ABC中,AB=AC=2$\sqrt{3}$,∠BAC=120°,$\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BC}$,则$\overrightarrow{AD}•\overrightarrow{AC}$=0.分析 用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AD}$,代入计算.
解答 解:$\overrightarrow{AD}•\overrightarrow{AC}$=($\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}$)$•\overrightarrow{AC}$=[$\overrightarrow{AB}+\frac{1}{3}(\overrightarrow{AC}-\overrightarrow{AB})$]$•\overrightarrow{AC}$=$\frac{2}{3}\overrightarrow{AB}•\overrightarrow{AC}$+$\frac{1}{3}$${\overrightarrow{AC}}^{2}$=$\frac{2}{3}$×$2\sqrt{3}×2\sqrt{3}×cos120°$+$\frac{1}{3}×(2\sqrt{3})^{2}$=0.
故答案为:0.
点评 本题考查了平面向量的数量积运算,是基础题.

练习册系列答案
相关题目
17.复数$\frac{i}{2-i}$在平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.程序框图如图所示,则该程序运行后输出的值是( )
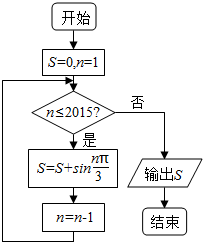

| A. | 0 | B. | $\sqrt{3}$ | C. | $-\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
18.已知实数x,y满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{kx-y+2≥0}\\{y≥0}\end{array}\right.$,且目标函数z=y-x取得最小值-4,则k等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -$\frac{1}{2}$ |
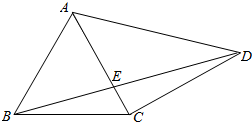 如图,△ABC是等边三角形,△ACD是等腰直角三角形,∠ACD=90°,BD交AC于E,AB=$\sqrt{2}$
如图,△ABC是等边三角形,△ACD是等腰直角三角形,∠ACD=90°,BD交AC于E,AB=$\sqrt{2}$