一个球由于某种原因其直径无法直接测量.有人设计了这么一个测量方法:把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切.沾到颜料的地方A.B就是切点.若量得|AB|=28.3cm.则此球的直径约为( )A．20cmB．40cmC．28.3cmD．34.6cm 题目和参考答案——青夏教育精英家教网—

题目内容

10．

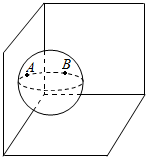一个球由于某种原因其直径无法直接测量，有人设计了这么一个测量方法：把球外面涂上颜料滚到一个房子的屋角使得球与两堵墙相切，沾到颜料的地方A，B就是切点（如图），若量得|AB|=28.3cm，则此球的直径约为（　　）

A．

20cm

B．

40cm

C．

28.3cm

D．

34.6cm

分析由题意可知，球心O与A，B的连线构成等腰直角三角形，由此求得球的直径．

解答解：如图，
△AOB为等腰直角三角形，|OA|=$\frac{\sqrt{2}}{2}$|AB|，
球的直径为2|OA|=$\sqrt{2}|AB|$
∵|AB|=28.3cm，
∴球的直径为$28.3\sqrt{2}$≈40cm．
故选：B．

点评本题考查旋转体表面上的最短距离问题，考查空间想象能力和思维能力，是中档题．

练习册系列答案

1．设常数a＞1，则f（x）=-x²-2ax+1在区间[-1，1]上的最大值为2a．

18．已知实数x，y满足$\left\{\begin{array}{l}{2x+y-2≥0}\\{kx-y+2≥0}\\{y≥0}\end{array}\right.$，且目标函数z=y-x取得最小值-4，则k等于（　　）

5．若对于任意实数t，圆C₁：（x+4）²+y²=1与圆C₂：（x-t）²+（y-at+2）²=1都没有公共点，则实数a的取值范围是a＜-$\frac{4}{3}$或a＞0．

15．设集合A={x|x²-x≤0}，B={0，1，2}，则A∩B=（　　）

2．计算2lg2+lg25+（$\sqrt{3}$）⁰=3．

19．

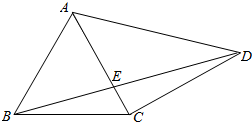如图，△ABC是等边三角形，△ACD是等腰直角三角形，∠ACD=90°，BD交AC于E，AB=$\sqrt{2}$
（Ⅰ）求∠BEA的度数；
（Ⅱ）求BD及AE的长．

20．下列函数中，随x的增大，其增大速度最快的是（　　）

y=x¹⁰⁰⁰

试题分类