题目内容
已知函数f(x)=2x2+mx-2m-3
(1)若函数在区间(-∞,0)与(1,+∞)内各有一个零点,求实数m的取值范围;
(2)若不等式f(x)≥(3m+1)x-3m-11在x∈(
,+∞)上恒成立,求实数m的取值范围.
(1)若函数在区间(-∞,0)与(1,+∞)内各有一个零点,求实数m的取值范围;
(2)若不等式f(x)≥(3m+1)x-3m-11在x∈(
| 1 |
| 2 |
考点:二次函数的性质,函数恒成立问题,函数零点的判定定理
专题:函数的性质及应用
分析:(1)由f(x)=2x2+mx-2m-3图象开口向上,且在区间(-∞,0)与(1,+∞)内各有一零点,故
,解得实数m的取值范围;
(2)解法一:若不等式f(x)≥(3m+1)x-3m-11在x∈(
,+∞)上恒成立,则2x2-(2m+1)x+m+8≥0在x∈(
,+∞)上恒成立,构造函数g(x)=2x2-(2m+1)x+m+8,(x>
)利用二次函数的图象和性质,可得答案;
解法二:若不等式f(x)≥(3m+1)x-3m-11在x∈(
,+∞)上恒成立,则m≤
=x+
,构造函数g(x)=x+
,(x>
),结合对勾函数的图象和性质求出最值,可得答案.
|
(2)解法一:若不等式f(x)≥(3m+1)x-3m-11在x∈(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解法二:若不等式f(x)≥(3m+1)x-3m-11在x∈(
| 1 |
| 2 |
| 2x2-x+8 |
| 2x-1 |
| 8 |
| 2x-1 |
| 8 |
| 2x-1 |
| 1 |
| 2 |
解答:
解:(1)由f(x)=2x2+mx-2m-3图象开口向上,且在区间(-∞,0)与(1,+∞)内各有一零点,
故
,----------------(3分)
即
,----------------(4分)
解得m>-1,即实数的取值范围为(-1,+∞);----------------(6分)
(2)方法一:不等式f(x)≥(3m-1)x-3m-11在x∈(
,+∞)上恒成立?2x2+mx-2m-3≥(3m-1)x-3m-11?2x2-(2m+1)x+m+8≥0----------------(7分)
取g(x)=2x2-(2m+1)x+m+8,(x>
)
对称轴x=
=m+
当m≤0时,对称轴x=m+
≤
∴g(x)在(
,+∞)上单调递增,g(x)>g(2)=8>0,
故m≤0满足题意----------------(9分)
当m>0时,对称轴x=m+
>
又g(x)≥0在(
,+∞)上恒成立,
故△=(2m+1)2-8(m+8)=4m2-4m-63=(2m+7)(2m-9)≤0
解得:-
≤m≤
,----------------(12分)
故0<m≤
----------------(13分)
综上所述,实数的取值范围为(-∞,
].----------------(14分)
方法二:不等式f(x)≥(3m-1)x-3m-11在x∈(
,+∞)上恒成立?2x2+mx-2m-3≥(3m-1)x-3m-11?m≤
=x+
----------------(9分)
取g(x)=x+
,(x>
)
由结论:定义在(0,+∞)上的函数h(x)=x+
,(a>0),当且仅当x=
时h(x)取得最小值2
.
故g(x)=x-
+
+
≥2
+
=
----------------(12分)
当且仅当x-
=2,即x=
时函数g(x)取得最小值
.----------------(13分)
故m≤
,即实数的取值范围为(-∞,
].----------------(14分)
故
|
即
|
解得m>-1,即实数的取值范围为(-1,+∞);----------------(6分)
(2)方法一:不等式f(x)≥(3m-1)x-3m-11在x∈(
| 1 |
| 2 |
取g(x)=2x2-(2m+1)x+m+8,(x>
| 1 |
| 2 |
对称轴x=
| 2m+1 |
| 2 |
| 1 |
| 2 |
当m≤0时,对称轴x=m+
| 1 |
| 2 |
| 1 |
| 2 |
∴g(x)在(
| 1 |
| 2 |
故m≤0满足题意----------------(9分)
当m>0时,对称轴x=m+
| 1 |
| 2 |
| 1 |
| 2 |
又g(x)≥0在(
| 1 |
| 2 |
故△=(2m+1)2-8(m+8)=4m2-4m-63=(2m+7)(2m-9)≤0
解得:-
| 7 |
| 2 |
| 9 |
| 2 |
故0<m≤
| 9 |
| 2 |
综上所述,实数的取值范围为(-∞,
| 9 |
| 2 |
方法二:不等式f(x)≥(3m-1)x-3m-11在x∈(
| 1 |
| 2 |
| 2x2-x+8 |
| 2x-1 |
| 8 |
| 2x-1 |
取g(x)=x+
| 8 |
| 2x-1 |
| 1 |
| 2 |
由结论:定义在(0,+∞)上的函数h(x)=x+
| a |
| x |
| a |
| a |
故g(x)=x-
| 1 |
| 2 |
| 4 | ||
x-
|
| 1 |
| 2 |
| 4 |
| 1 |
| 2 |
| 9 |
| 2 |
当且仅当x-
| 1 |
| 2 |
| 5 |
| 2 |
| 9 |
| 2 |
故m≤
| 9 |
| 2 |
| 9 |
| 2 |
点评:本题考查的知识点是二次函数的图象和性质,函数恒成立问题,函数的零点,是函数图象和性质的综合应用,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=x2-x+2在下列哪个区间上是单调减函数( )
| A、(0,+∞) |
| B、(-∞,0) |
| C、(1,+∞) |
| D、(-∞,1) |
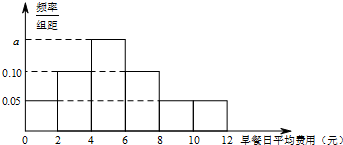 某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如图所示的频率分布直方图,图中标注a的数字模糊不清.
某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如图所示的频率分布直方图,图中标注a的数字模糊不清.