题目内容
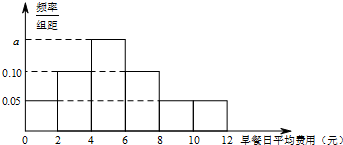 某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如图所示的频率分布直方图,图中标注a的数字模糊不清.
某公司为了了解本公司职员的早餐费用情况,抽样调査了100位职员的早餐日平均费用(单位:元),得到如图所示的频率分布直方图,图中标注a的数字模糊不清. (1)试根据频率分布直方图求a的值,并估计该公司职员早餐日平均费用的众数;
(2)已知该公司有1000名职员,试估计该公司有多少职员早餐日平均费用不少于8元?
考点:频率分布直方图
专题:
分析:(1)由频率分布直方图中各小长方形的面积之和等于1,求出a的值,频率分布直方图中最高的小长方体的底面边长的中点即是众数;
(2)求出本公司职员平均费用不少于8元的频率就能求出公司有多少职员早餐日平均费用不少于8元.
(2)求出本公司职员平均费用不少于8元的频率就能求出公司有多少职员早餐日平均费用不少于8元.
解答:
解:(1)据题意得:(0.05+0.10+a+0.10+0.05+0.05)×2=1,
解得a=0.15,
众数为:
=5;
(2)该公司职员早餐日平均费用不少于8元的有:
(
×0.05+
×0.05)×1000=100,
∴频率分布直方图求a的值为0.15,该公司职员早餐日平均费用的众数为5;
(2)该公司有职员早餐日平均费用不少于8元的有100.
解得a=0.15,
众数为:
| 4+6 |
| 2 |
(2)该公司职员早餐日平均费用不少于8元的有:
(
| 8+10 |
| 2 |
| 10+12 |
| 2 |
∴频率分布直方图求a的值为0.15,该公司职员早餐日平均费用的众数为5;
(2)该公司有职员早餐日平均费用不少于8元的有100.
点评:本题考查频率分布直方图的应用,注意频率=纵坐标×组距,属于一道基础题.

练习册系列答案
相关题目
已知函数f(x)=(x+α)cosx为奇函数,则a= ;现将函数f(x)的图象沿x轴向左平移
个单位,得到的图象所对应的函数记为g(x),那么其解析式g(x)= ;且函数g(x)图象的对称中心为 .
| π |
| 2 |
A、B是锐角三角形的两个内角,则直线xsinA-ycosB=0的倾斜角( )
| A、大于135° |
| B、大于90°且小于135° |
| C、大于45°且小于90° |
| D、小于45° |