题目内容
5.已知关于x的方程$\frac{1}{2}$x2-2lnx=m在区间[$\frac{1}{e}$,e]上有实数解,求m的范围.分析 令f(x)=$\frac{1}{2}$x2-2lnx,利用导数法求出函数的最值,进而可得关于x的方程$\frac{1}{2}$x2-2lnx=m在区间[$\frac{1}{e}$,e]上有实数解时,m的范围.
解答 解:令f(x)=$\frac{1}{2}$x2-2lnx,
则f′(x)=x-$\frac{2}{x}$=$\frac{{x}^{2}-2}{x}$,
当x∈[$\frac{1}{e}$,$\sqrt{2}$)时,f′(x)<0,f(x)为减函数,x∈[$\sqrt{2}$,e]时,f′(x)>0,f(x)为增函数,
故当x=$\sqrt{2}$时,f(x)取最小值1-ln2,
又由x=$\frac{1}{e}$时,f(x)=$\frac{1}{2{e}^{2}}+2$,x=2时,f(x)=$\frac{{e}^{2}}{2}-2$,
故x=$\frac{1}{e}$时,f(x)取最大值$\frac{1}{2{e}^{2}}+2$,
若x的方程$\frac{1}{2}$x2-2lnx=m在区间[$\frac{1}{e}$,e]上有实数解,
m∈[1-ln2,$\frac{1}{2{e}^{2}}+2$]
点评 本题考查的知识点是函数的零点的判定定理,函数的值域,难度中档.

练习册系列答案
相关题目
15.下列函数在(0,+∞)上是减函数的是( )
| A. | y=x2 | B. | y=-x2 | C. | y=-2x2+3x-1 | D. | y=x |
15.若2cos($\frac{π}{2}$-α)-sin($\frac{3}{2}$π+α)=-$\sqrt{5}$,则tanα=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
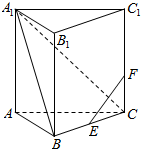 如图,已知直三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,点F在侧棱CC1上,且CF=1,求证:EF⊥A1C.
如图,已知直三棱柱ABC-A1B1C1的各棱长都是4,E是BC的中点,点F在侧棱CC1上,且CF=1,求证:EF⊥A1C.