Question

16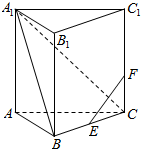．如图，已知直三棱柱ABC-A₁B₁C₁的各棱长都是4，E是BC的中点，点F在侧棱CC₁上，且CF=1，求证：EF⊥A₁C．

Answer 1

分析 以A为原点，在平面ABC中作AC的垂线为x轴，AC为y轴，AA₁为z轴，建立空间直角坐标系，利用向量法能证明EF⊥A₁C．

解答 证明：以A为原点，在平面ABC中作AC的垂线为x轴，AC为y轴，AA₁为z轴，建立空间直角坐标系，
∵直三棱柱ABC-A₁B₁C₁的各棱长都是4，E是BC的中点，点F在侧棱CC₁上，且CF=1，
∴A₁（0，0，4），C（0，4，0），E（$\sqrt{3}$，3，0），F（0，4，1），
∴$\overrightarrow{EF}$=（-$\sqrt{3}$，1，1），$\overrightarrow{{A}_{1}C}$=（0，4，-4），
∴$\overrightarrow{EF}•\overrightarrow{{A}_{1}C}$=0+4-4=0，
∴EF⊥A₁C．

点评 本题考查异面直线垂直的证明，是中档题，解题时要认真审题，注意向量法的合理运用．