题目内容
 近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-
近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-| 1 |
| 10 |
(Ⅰ)促销活动的第30天,网店获得的利润为多少万元?
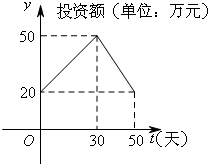
(Ⅱ)请你写出网店的投资额g(t)与促销时间t之间的关系式;
(Ⅲ)在促销活动的前30天内,哪一天的销售利润最大?最大利润是多少万元?
考点:函数模型的选择与应用
专题:应用题,函数的性质及应用
分析:(Ⅰ)利用网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-
t(t-60),可得结论;
(Ⅱ)根据函数的图象,可得网店的投资额g(t)与促销时间t之间的关系式;
(Ⅲ)求出函数表达式,利用配方法,可得结论.
| 1 |
| 10 |
(Ⅱ)根据函数的图象,可得网店的投资额g(t)与促销时间t之间的关系式;
(Ⅲ)求出函数表达式,利用配方法,可得结论.
解答:
解:(Ⅰ)利用网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-
t(t-60),可得促销活动的第30天,网店的销售额f(30)=-
×30(30-60)=90万元,投资额g(30)=50万元,
∴网店获得的利润为40元;
(Ⅱ)0≤t≤30时,g(t)=t+20,30<t≤50,g(t)=-1.5t+95;
(Ⅲ)0≤t≤30时,L=f(t)-g(t)
=-
t(t-60)-t-20=-
(t-25)2+42.5,
∴t=25时,利润最大为42.5万元.
| 1 |
| 10 |
| 1 |
| 10 |
∴网店获得的利润为40元;
(Ⅱ)0≤t≤30时,g(t)=t+20,30<t≤50,g(t)=-1.5t+95;
(Ⅲ)0≤t≤30时,L=f(t)-g(t)
=-
| 1 |
| 10 |
| 1 |
| 10 |
∴t=25时,利润最大为42.5万元.
点评:本题考查函数模型的选择与应用,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 已知五棱锥P-ABCDE中,PA⊥平面ABCDE,五边形ABCDE中,BA⊥AE,AB⊥BC,AB=2
已知五棱锥P-ABCDE中,PA⊥平面ABCDE,五边形ABCDE中,BA⊥AE,AB⊥BC,AB=2 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB. 已知椭圆C:
已知椭圆C: 如图,一个圆锥形容器的高为a,内装有一定量的水.如果将容器倒置,这时所形成的圆锥的高恰为
如图,一个圆锥形容器的高为a,内装有一定量的水.如果将容器倒置,这时所形成的圆锥的高恰为