题目内容
已知(
-
)n展开式中第三项的系数是144.
(1)求n的值;
(2)求展开式中含x3的项.
| x |
| 2 |
| x |
(1)求n的值;
(2)求展开式中含x3的项.
考点:二项式系数的性质
专题:二项式定理
分析:(1)依题意,利用二项式的通项公式可求得n的值;
(2)设第r+1项为含x3的项,利用二项式的通项公式可求得r=1,从而可求得展开式中含x3的项.
(2)设第r+1项为含x3的项,利用二项式的通项公式可求得r=1,从而可求得展开式中含x3的项.
解答:
解:(1)T3=
(
)n-2(-
)2=4
x
,…3分
依题意得4
=144,∴n=9…6分
(2)设第r+1项为含x3的项,则
(
)9-r(-
)r=(-2)r
x
,…8分
令
=3,r=1,…10分
∴第二项为含x3的项,T2=-2
x3=-18x3…12分
| C | 2 n |
| x |
| 2 |
| x |
| C | 2 n |
| n-4 |
| 2 |
依题意得4
| C | 2 n |
(2)设第r+1项为含x3的项,则
| C | r 9 |
| x |
| 2 |
| x |
| C | r 9 |
| 9-3r |
| 2 |
令
| 9-3r |
| 2 |
∴第二项为含x3的项,T2=-2
| C | 1 9 |
点评:本题考查二项式系数的性质,着重考查二项式的通项公式及其应用,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在四棱锥P-ABCD中,地面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点.
如图,在四棱锥P-ABCD中,地面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点. 如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠ADC=90°,AB∥CD,AD=AF=a,AB=2CD=2a.
如图,已知平面ABEF⊥平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,∠ADC=90°,AB∥CD,AD=AF=a,AB=2CD=2a.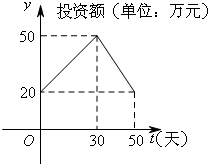 近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-
近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-