题目内容
如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD=2AE，AE⊥AB．（Ⅰ）若F为CD中点，证明：EF∥平面ABC；
（Ⅱ）若AB=BD，求直线EB与平面BCD所成角的余弦值．
考点：直线与平面所成的角,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（Ⅰ）取BD中点G，连结EG，GF，由已知条件推导出EG∥AB，GF∥BC，由此证明平面EFG∥平面ABC，从而得到EF∥平面ABC．
（Ⅱ）连结BF，则∠EBF为直线EB与平面BCD所成角，由此能求出直线EB与平面BCD所成角的余弦值．
（Ⅱ）连结BF，则∠EBF为直线EB与平面BCD所成角，由此能求出直线EB与平面BCD所成角的余弦值．
解答：
（Ⅰ）证明：取BD中点G，连结EG，GF，
∵等边△ABC与直角梯形ABDE所在平面垂直，
BD∥AE，BD=2AE，AE⊥AB，
∴AE
CB，∴ABGE是平行四边形，∴EG∥AB，
∵F为CD中点，∴GF∥BC，
∵EG，GF?平面，EG∩FG=G，
∴平面EFG∥平面ABC，
∵EF?平面平面EFG，∴EF∥平面ABC．
（Ⅱ）解：∵等边△ABC与直角梯形ABDE所在平面垂直，
BD∥AE，BD=2AE，AE⊥AB，G是BD中点，
∴EF⊥GF，EF⊥BD，∴EF⊥平面BDC，
连结BF，则∠EBF为直线EB与平面BCD所成角，
由题意知设BD=2AE=2，
则BF=
=
，BE=
=
，
∴cos∠EBF=
=
=
，
∴直线EB与平面BCD所成角的余弦值为
．
∵等边△ABC与直角梯形ABDE所在平面垂直，
BD∥AE，BD=2AE，AE⊥AB，
∴AE
| ∥ |
. |
∵F为CD中点，∴GF∥BC，
∵EG，GF?平面，EG∩FG=G，
∴平面EFG∥平面ABC，
∵EF?平面平面EFG，∴EF∥平面ABC．
（Ⅱ）解：∵等边△ABC与直角梯形ABDE所在平面垂直，
BD∥AE，BD=2AE，AE⊥AB，G是BD中点，
∴EF⊥GF，EF⊥BD，∴EF⊥平面BDC，
连结BF，则∠EBF为直线EB与平面BCD所成角，
由题意知设BD=2AE=2，
则BF=
| 12+12 |
| 2 |
| 12+22 |
| 5 |
∴cos∠EBF=
| BF |
| BE |
| ||
|
| ||
| 5 |
∴直线EB与平面BCD所成角的余弦值为
| ||
| 5 |
点评：本题考查直线与平面平行的证明，考查直线与平面所成角的余弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
优生乐园系列答案
相关题目
如图，在四边形ABCD中，AB∥CD，∠ABD=30°，AB=2CD=2AD=2DE=2，DE⊥平面ABCD，EF∥BD，且BD=2EF．
如图，已知平面ABEF⊥平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠ADC=90°，AB∥CD，AD=AF=a，AB=2CD=2a．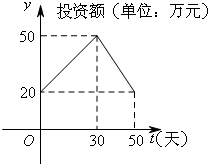
近年来，网上购物已经成为人们消费的一种趋势．为了获得更多的利润，某网店在国庆节前后搞了一次长达50天的促销活动．在这50天内，网店的销售额（单位：万元）与促销时间（单位：天）的关系满足f（t）=-