题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设A、B是椭圆上位于x轴上方的两点,且直线AF1与直线BF2平行,AF2与BF1交于点P.试用|AF1|,|BF2|表示|PF1|+|PF2|,并证明|PF1|+|PF2|是定值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由题设知c=1,由点(1,e)在椭圆上,得
+
=1,求出b,即可求椭圆C的方程.
(Ⅱ)设AF1与BF2的方程分别为x+1=my,x-1=my,与椭圆方程联立,求出|AF1|、|BF2|,利用直线AF1与直线BF2平行,点B在椭圆上知,可PF1=
×(2
-BF2),同理PF2=
×(2
-AF1),由此可求得PF1+PF2是定值.
| 1 |
| a2 |
| e2 |
| b2 |
(Ⅱ)设AF1与BF2的方程分别为x+1=my,x-1=my,与椭圆方程联立,求出|AF1|、|BF2|,利用直线AF1与直线BF2平行,点B在椭圆上知,可PF1=
| AF1 |
| AF1+BF2 |
| 2 |
| BF2 |
| AF1+BF2 |
| 2 |
解答:
解:(Ⅰ)由题设知c=1,由点(1,e)在椭圆上,得
+
=1,∴b=1,a=
.
∴椭圆的方程为
+y2=1.
(Ⅱ)∵直线AF1与直线BF2平行,∴设AF1与BF2的方程分别为x+1=my,x-1=my.
设A(x1,y1),B(x2,y2),y1>0,y2>0,
∴由
,可得(m2+2)y12-2my1-1=0.
∴y1=
,
∴|AF1|=
×|0-y1|=
①
同理|BF2|=
②
∵直线AF1与直线BF2平行,∴
=
,即PF1=
×BF1.
由点B在椭圆上知,BF1+BF2=2
,∴PF1=
×(2
-BF2).
同理PF2=
×(2
-AF1).
∴|PF1|+|PF2|=
×(2
-BF2)+
×(2
-AF1)=2
-
.
由①②得,|AF1|+|BF2|=
,|AF1||BF2|=
,
∴|PF1|+|PF2|=
.
∴PF1+PF2是定值.
| 1 |
| a2 |
| e2 |
| b2 |
| 2 |
∴椭圆的方程为
| x2 |
| 2 |
(Ⅱ)∵直线AF1与直线BF2平行,∴设AF1与BF2的方程分别为x+1=my,x-1=my.
设A(x1,y1),B(x2,y2),y1>0,y2>0,
∴由
|
∴y1=
m+
| ||
| m2+2 |
∴|AF1|=
| m2+1 |
| ||||
| m2+2 |
同理|BF2|=
| ||||
| m2+2 |
∵直线AF1与直线BF2平行,∴
| PB |
| PF1 |
| BF2 |
| AF1 |
| AF1 |
| AF1+BF2 |
由点B在椭圆上知,BF1+BF2=2
| 2 |
| AF1 |
| AF1+BF2 |
| 2 |
同理PF2=
| BF2 |
| AF1+BF2 |
| 2 |
∴|PF1|+|PF2|=
| AF1 |
| AF1+BF2 |
| 2 |
| BF2 |
| AF1+BF2 |
| 2 |
| 2 |
| 2AF1×BF2 |
| AF1+BF2 |
由①②得,|AF1|+|BF2|=
2
| ||
| m2+2 |
| m2+1 |
| m2+2 |
∴|PF1|+|PF2|=
3
| ||
| 2 |
∴PF1+PF2是定值.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于难题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.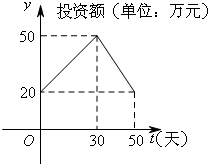 近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-
近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-