题目内容
 如图,一个圆锥形容器的高为a,内装有一定量的水.如果将容器倒置,这时所形成的圆锥的高恰为
如图,一个圆锥形容器的高为a,内装有一定量的水.如果将容器倒置,这时所形成的圆锥的高恰为| a |
| 2 |
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:设图①中的小圆锥的底面半径为r,则大圆锥的底面半径为2r,求出水的体积;再设图②中的小圆锥的底面半径为m,高为h,则,先由相似知识求出m,再由棱锥的体积公式求出水的体积,再由体积相等,解出高h即可.
解答:
 解:设图①中的小圆锥的底面半径为r,则大圆锥的底面半径为2r,水的体积为V=
解:设图①中的小圆锥的底面半径为r,则大圆锥的底面半径为2r,水的体积为V=
π•4r2•a-
πr2•
=
πr2•a,
设图②中的小圆锥的底面半径为m,高为h,则,由相似知识得,
=
,m=
,
则水的体积为V=
π•
•h
即有
πr2•a=
π•
•h,
解得h=
a,
故答案为:
a.
 解:设图①中的小圆锥的底面半径为r,则大圆锥的底面半径为2r,水的体积为V=
解:设图①中的小圆锥的底面半径为r,则大圆锥的底面半径为2r,水的体积为V=| 1 |
| 3 |
| 1 |
| 3 |
| a |
| 2 |
| 7 |
| 6 |
设图②中的小圆锥的底面半径为m,高为h,则,由相似知识得,
| m |
| 2r |
| h |
| a |
| 2rh |
| a |
则水的体积为V=
| 1 |
| 3 |
| 4r2h2 |
| a2 |
即有
| 7 |
| 6 |
| 1 |
| 3 |
| 4r2h2 |
| a2 |
解得h=
| |||
| 2 |
故答案为:
| |||
| 2 |
点评:本题考查棱锥的体积公式的运用,以及等积法的应用,考查运算的能力,属于基础题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
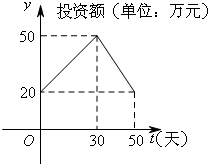 近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-
近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-