题目内容
设函数f(x)=x-1-
.
(Ⅰ)令N(x)=x2-1+lnx,判断N(x)在(0,+∞)上的单调性并求所有的零点;
(Ⅱ)求f(x)在定义域上的最小值;
(Ⅲ)求证:对任意n∈N*,n≥2,都有:
+
+
+…
>1-
.
| lnx |
| x |
(Ⅰ)令N(x)=x2-1+lnx,判断N(x)在(0,+∞)上的单调性并求所有的零点;
(Ⅱ)求f(x)在定义域上的最小值;
(Ⅲ)求证:对任意n∈N*,n≥2,都有:
| 1 |
| ln2 |
| 1 |
| ln3 |
| 1 |
| ln4 |
| 1 |
| lnn |
| 1 |
| n |
考点:利用导数求闭区间上函数的最值,函数零点的判定定理,利用导数研究函数的单调性
专题:计算题,导数的概念及应用
分析:(Ⅰ)求导判定N(x)单调性,再求零点;
(Ⅱ)求导找到最小值;
(Ⅲ)由f(x)≥0推
>
=
=
-
,得解.
(Ⅱ)求导找到最小值;
(Ⅲ)由f(x)≥0推
| 1 |
| lnk |
| 1 |
| k2-k |
| 1 |
| k(k-1) |
| 1 |
| k-1 |
| 1 |
| k |
解答:
解:(Ⅰ)∵N′(x)=2x+
>0,
∴N(x)在(0,+∞)上单调递增;
那么N(x)在(0,+∞)上至多有一个零点,
由N(1)=1-1+0=0,则N(x)在(0,+∞)上唯一零点为x=1.
(Ⅱ)f(x)的定义域为(0,+∞);
f′(x)=1-
=
,
则①当0<x<1时,N(x)<0,则f′(x)<0,
②当x>1时,N(x)>0,则f′(x)>0,
则f(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
则f(x)min=f(1)=0.
(Ⅲ)由f(x)=x-1-
≥0可得,
x2-x≥lnx(x>0)
令x=k≥2,
则k2-k>0,lnk>0,k2-k>lnk;
则
>
=
=
-
则
+
+
+…
>
-
+
-
+…+
-
=1-
.
| 1 |
| x |
∴N(x)在(0,+∞)上单调递增;
那么N(x)在(0,+∞)上至多有一个零点,
由N(1)=1-1+0=0,则N(x)在(0,+∞)上唯一零点为x=1.
(Ⅱ)f(x)的定义域为(0,+∞);
f′(x)=1-
| 1-lnx |
| x2 |
| N(x) |
| x2 |
则①当0<x<1时,N(x)<0,则f′(x)<0,
②当x>1时,N(x)>0,则f′(x)>0,
则f(x)在(0,1)上单调递减,在(1,+∞)上单调递增;
则f(x)min=f(1)=0.
(Ⅲ)由f(x)=x-1-
| lnx |
| x |
x2-x≥lnx(x>0)
令x=k≥2,
则k2-k>0,lnk>0,k2-k>lnk;
则
| 1 |
| lnk |
| 1 |
| k2-k |
| 1 |
| k(k-1) |
| 1 |
| k-1 |
| 1 |
| k |
则
| 1 |
| ln2 |
| 1 |
| ln3 |
| 1 |
| ln4 |
| 1 |
| lnn |
| 1 |
| 1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n |
点评:本题综合性很强,考查了导数的综合应用,零点个数的判定,不等式的证明及裂项求和的方法,属于难题.

练习册系列答案
相关题目
 如图,在四边形ABCD中,AB∥CD,∠ABD=30°,AB=2CD=2AD=2DE=2,DE⊥平面ABCD,EF∥BD,且BD=2EF.
如图,在四边形ABCD中,AB∥CD,∠ABD=30°,AB=2CD=2AD=2DE=2,DE⊥平面ABCD,EF∥BD,且BD=2EF. 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°. 如图,在四棱锥P-ABCD中,地面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点.
如图,在四棱锥P-ABCD中,地面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点.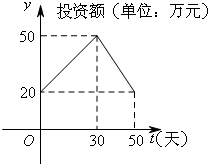 近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-
近年来,网上购物已经成为人们消费的一种趋势.为了获得更多的利润,某网店在国庆节前后搞了一次长达50天的促销活动.在这50天内,网店的销售额(单位:万元)与促销时间(单位:天)的关系满足f(t)=-