题目内容
点A(3,
),B(-8,-2)分别在幂函数y=f(x)和y=g(x)的图象上,且f(x)<g(x),求实数x的取值范围.
| 3 | 27 |
考点:其他不等式的解法,幂函数的概念、解析式、定义域、值域,幂函数的性质
专题:函数的性质及应用,不等式的解法及应用
分析:利用幂函数图象结果的点,求出函数的解析式,然后结合不等式求解即可.
解答:
 解:A(3,
解:A(3,
)即A(3,3)在幂函数y=f(x)的图象上,所以f(x)=x.
B(-8,-2)在幂函数y=g(x)的图象上,-2=(-8)a,解得a=
,g(x)=x
.
f(x)<g(x),即x<x
,化为:x3<x,
可得x(x2-1)<0.解得x<-1或0<x<1.
实数x的取值范围:{x|x<-1或0<x<1}.
 解:A(3,
解:A(3,| 3 | 27 |
B(-8,-2)在幂函数y=g(x)的图象上,-2=(-8)a,解得a=
| 1 |
| 3 |
| 1 |
| 3 |
f(x)<g(x),即x<x
| 1 |
| 3 |
可得x(x2-1)<0.解得x<-1或0<x<1.
实数x的取值范围:{x|x<-1或0<x<1}.
点评:本题考查幂函数的极限的求法,高次不等式的解法,考查分析问题解决问题的能力.函数的图象的应用.

练习册系列答案
相关题目
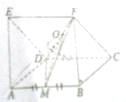 如图,在直三棱柱ADE-BCF中,面ABFE和面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运动向量方法证明:
如图,在直三棱柱ADE-BCF中,面ABFE和面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运动向量方法证明: