题目内容
三棱锥S-ABC中，SA=AB=AC=2，∠ASB=∠BSC=∠CSA=30°，M，N分别为SB，SC上的点，则△AMN周长最小值为 ．
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：沿着侧棱SA把正三棱锥展开在同一个平面内，原来的点A被分到两处A，A′，则线段AA′的长度即为△AMN周长的最小值．
解答：
解：沿着侧棱SA把正三棱锥展开在同一个平面内，
原来的点A被分到两处A，A′，
则线段AA′的长度即为△AMN周长的最小值．
△SAA′中，SA=SA′=2，∠ASB=∠BSC=∠CSA=30°，
故∠ASA′=90°，
∴AA′=
=
=2
．
故答案为：2
．
原来的点A被分到两处A，A′，
则线段AA′的长度即为△AMN周长的最小值．
△SAA′中，SA=SA′=2，∠ASB=∠BSC=∠CSA=30°，
故∠ASA′=90°，
∴AA′=
| SA2+SA′2 |
| 4+4 |
| 2 |
故答案为：2
| 2 |
点评：本题考查三角形周长的最小值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
函数f（x）=
（x∈[1，2]）的最大值是（ ）
| 1 |
| 1-x+x2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
现有四个函数：①y=x•sinx；②y=x•cosx；③y=x•|cosx|；④y=x•2x的图象（部分）如下：
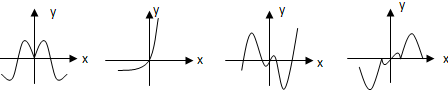
则按照从左到右图象对应的函数序号安排正确的一组是（ ）
则按照从左到右图象对应的函数序号安排正确的一组是（ ）
| A、①④③② | B、③④②① |
| C、④①②③ | D、①④②③ |