题目内容
如图10-22,在正三棱柱ABC—A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为 ,设这条最短路线与CC1的交点为N。
,设这条最短路线与CC1的交点为N。
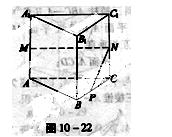
求:(1)该三棱柱侧面展开图的对角线长;
(2)PC与NC的长;
(3)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示)。

 角)。在Rt△PHC中,∵∠PCH=
角)。在Rt△PHC中,∵∠PCH= ∠PCP1=60°,∴CH=
∠PCP1=60°,∴CH= 、在Rt△NCH中tan∠NHC=
、在Rt△NCH中tan∠NHC= ∠NHC=arctan
∠NHC=arctan ∴平面NMP与平面ABC所成二面角(锐角)的大小为arctan
∴平面NMP与平面ABC所成二面角(锐角)的大小为arctan 。
。
解法2:∵△MPN在△ABC上的射影为△APC,设所求的角为θ则cosθ= .故平面NMP与平面ABC所成二面角(锐角)的大小为arccos
.故平面NMP与平面ABC所成二面角(锐角)的大小为arccos .
.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目

 =___________。
=___________。 则
则 的最大值是______.
的最大值是______. ,圆心在直线
,圆心在直线 上,圆被直线
上,圆被直线 截得的弦长为
截得的弦长为 ,则圆的标准方程为
,则圆的标准方程为 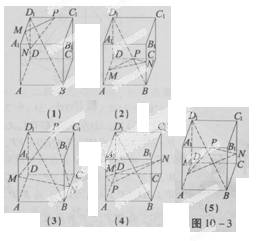
 是两条不同直线,
是两条不同直线, 是三个不同平面,下列命题中正确的是( )
是三个不同平面,下列命题中正确的是( ) B.
B.
 D.
D.
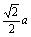 ,D是A1C1的中点。
,D是A1C1的中点。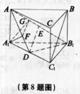
 ,学号依次为1,2,3,…,56,现用系统抽样的办法抽取一个容量为4的样本.已知学号为6,34,48的同学在样本中,那么还有一个同学的学号应为_____
,学号依次为1,2,3,…,56,现用系统抽样的办法抽取一个容量为4的样本.已知学号为6,34,48的同学在样本中,那么还有一个同学的学号应为_____ ___.
___.