题目内容
设等比数列{an}的公比为q，前n项和为Sn．若Sn+1=4Sn-3，则q= ，a1= ．
考点：等比数列的前n项和
专题：等差数列与等比数列
分析：由Sn+1=4Sn-3，得an+1=4an，从而q=
=4．当n=1时，a2=3a1-3，又a2=4a1，由此得a1=-3．
| an+1 |
| an |
解答：
解：∵等比数列{an}的公比为q，前n项和为Sn．
Sn+1=4Sn-3，①
∴n≥2时，Sn=4Sn-1-3，②
①-②，得an+1=4an，∴q=
=4．
当n=1时，Sn+1=a1+a2=4a1-3，
整理，得a2=3a1-3，
又a2=4a1，∴4a1=3a1-3，
解得a1=-3．
故答案为：4；-3．
Sn+1=4Sn-3，①
∴n≥2时，Sn=4Sn-1-3，②
①-②，得an+1=4an，∴q=
| an+1 |
| an |
当n=1时，Sn+1=a1+a2=4a1-3，
整理，得a2=3a1-3，
又a2=4a1，∴4a1=3a1-3，
解得a1=-3．
故答案为：4；-3．
点评：本题考查等比数列的首项和公比的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．
练习册系列答案
相关题目
若直线l经过点A（4，2），B（6，3），则直线l的斜率为（ ）
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
已知集合A={x|x＜2}，B={y|y=5x}，则A∩B=（ ）
| A、{x|x＜2} |
| B、{x|x＞2} |
| C、{x|o≤x＜2} |
| D、{x|0＜x＜2} |
假设某设备的使用年限x（年）和所支出的维修费用y（元）呈线性相关关系，且有如下的统计资料：
则x和y之间的线性回归方程为（ ）
| 使用年限x（年） | 2 | 3 | 4 | 5 | 6 |
| 维修费用y（元） | 2.2 | 3.8 | 5.5 | 6.5 | 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
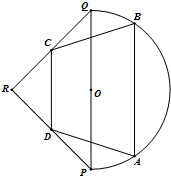如图，我市有一个健身公园，由一个直径为2km的半圆和一个以PQ为斜边的等腰直角三角形△PRQ构成，其中O为PQ的中点．现准备在公园里建设一条四边形健康跑道ABCD，按实际需要，四边形ABCD的两个顶点C、D分别在线段QR、PR上，另外两个顶点A、B在半圆上，AB∥CD∥PQ，且AB、CD间的距离为1km．设四边形ABCD的周长为ckm．